
【题目】如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1).
(1)以O点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出图形;
(2)B点的对应点B′的坐标是 ;C点的对应点C′的坐标是 ;
(3)在BC上有一点P(x,y),按(1)的方式得到的对应点P′的坐标是 .

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料,并用相关的思想方法解决问题.材料:为解方程x4﹣x2﹣6=0可将方程变形为(x2)2﹣x2﹣6=0然后设x2=y,则(x2)2=y2,原方程化为y2﹣y﹣6=0…①
解得y1=﹣2,y2=3,当y1=﹣2时,x2=﹣2无意义,舍去;
当y2=3时,x2=﹣3,解得x=±![]() ;
;
所以原方程的解为x1=![]() ,x2=﹣
,x2=﹣![]() ;
;
问题:(1)在原方程得到方程①的过程中,利用 法达到了降次的目的,体现了 的数学思想;
(2)利用以上学习到的方法解下列方程(x2+5x+1)(x2+5x+7)=7.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是等腰Rt△ABC外一点,把线段BP绕点B顺时针旋转90°得到线段BP',已知∠AP'B=135°,P'A:P'C=1:3,则P'A:PB=_____.
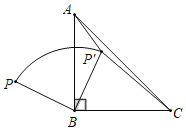
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过A(-3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l与x轴交于点H.
经过A(-3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l与x轴交于点H.
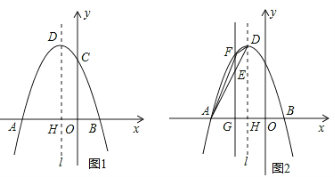
(1)求该抛物线的解析式;
(2)若点P是该抛物线对称轴l上的一个动点,求△PBC周长的最小值;
(3)如图(2),若E是线段AD上的一个动点( E与A、D不重合),过E点作平行于y轴的直线交抛物线于点F,交x轴于点G,设点E的横坐标为m,△ADF的面积为S.
①求S与m的函数关系式;
②S是否存在最大值?若存在,求出最大值及此时点E的坐标; 若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②a+b+c<0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根.其中正确结论是________.
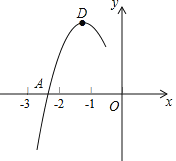
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点.
点.
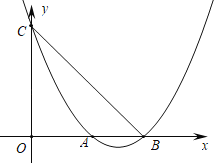
(1)求![]() 、
、![]() 、
、![]() 三点坐标;
三点坐标;
(2)求过![]() 、
、![]() 两点的一次函数的解析式;
两点的一次函数的解析式;
(3)如果![]() 是线段
是线段![]() 上的动点,试求
上的动点,试求![]() 的面积
的面积![]() 与
与![]() 之间的关系式.
之间的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现, 销售量y(件)与销售单价x(元)符合一次函数,所调查的部分数据如表:
销售单价x(元) | 65 | 70 | 80 | … |
销售量y(件) | 55 | 50 | 40 | … |
(1)求出y与x之间的函数表达式;
(2)若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少?
(3)销售单价定为多少元时,该商场获得的利润恰为500元?
查看答案和解析>>
科目:初中数学 来源: 题型:
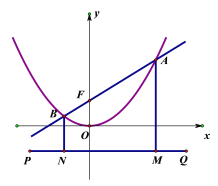
【题目】已知直线l:y=kx+4与抛物线y=![]() x2交于点A(x1,y1),B(x2,y2).
x2交于点A(x1,y1),B(x2,y2).
(1)求:![]() ;
;![]() 的值.
的值.
(2)过点(0,-4)作直线PQ∥x轴,且过点A、B分别作AM⊥PQ于点M,BN⊥PQ于点N,设直线l:y=kx+4交y轴于点F.求证:AF=AM=4+y1.
(3)证明:![]() +
+![]() 为定值,并求出该值.
为定值,并求出该值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】爱动脑筋的小明在学过用配方法解一元二次方程后,他发现二次三项式也可以配方,从而解决一些问题.
例如:![]()
![]() ;因此
;因此![]() 有最小值是1,只有当
有最小值是1,只有当![]() 时,才能得到这个式子的最小值1.
时,才能得到这个式子的最小值1.
同样![]() ,因此
,因此![]() 有最大值是8,只有当
有最大值是8,只有当![]() 时,才能得到这个式子的最大值8.
时,才能得到这个式子的最大值8.
(1)当x= 时,代数式﹣2(x﹣3)2+5有最大值为 .
(2)当x= 时,代数式2x2+4x+3有最小值为 .
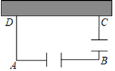
(3)矩形自行车场地ABCD一边靠墙(墙长10m),在AB和BC边各开一个1米宽的小门(不用木板),现有能围成14m长的木板,当AD长为多少时,自行车场地的面积最大?最大面积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com