
����Ŀ����ͼ����֪������![]() ����A����3��0����B��1��0����C��0��3�����㣬�䶥��ΪD���Գ�����ֱ��l��l��x�ύ�ڵ�H��
����A����3��0����B��1��0����C��0��3�����㣬�䶥��ΪD���Գ�����ֱ��l��l��x�ύ�ڵ�H��
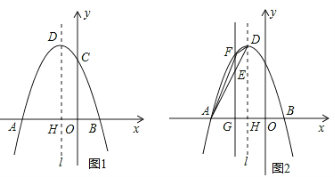
��1����������ߵĽ���ʽ��
��2������P�Ǹ������߶Գ���l�ϵ�һ�����㣬����PBC�ܳ�����Сֵ��
��3����ͼ��2������E���߶�AD�ϵ�һ�����㣨 E��A��D���غϣ�����E����ƽ����y���ֱ�߽��������ڵ�F����x���ڵ�G�����E�ĺ�����Ϊm����ADF�����ΪS��
����S��m�ĺ�����ϵʽ��
��S�Ƿ�������ֵ�������ڣ�������ֵ����ʱ��E�����ꣻ �������ڣ���˵�����ɣ�
���𰸡��⣺��1����������![]() ����A����3��0����B��1��0����
����A����3��0����B��1��0����
�����������߽���ʽΪ![]() ��
��
����������![]() ����C��0��3������
����C��0��3������![]() ��
��
�������ߵĽ���ʽΪ��![]() ����
����![]() ��
��
��2���ߡ�PBC���ܳ�Ϊ��PB+PC+BC����BC�Ƕ�ֵ��
����PB+PC��Сʱ����PBC���ܳ���С��
����A����B���ڶԳ���I�Գƣ�
������AC��l�ڵ�P������PΪ����ĵ㡣
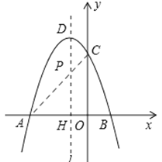
��AP=BP�����PBC���ܳ���С�ǣ�PB+PC+BC=AC+BC��
��A����3��0����B��1��0����C��0��3������AC=3![]() ��BC=
��BC=![]() ��
��
���PBC���ܳ���С�ǣ�![]() ��
��
��3���١�������![]() ����D������Ϊ����1��4����A����3��0����
����D����������1��4����A����3��0����
��ֱ��AD�Ľ���ʽΪy=2x+6
����E�ĺ�����Ϊm����E��m��2m+6����F��m��![]() ��
��
��![]() ��
��
��![]() ��
��
��S��m�ĺ�����ϵʽΪ![]() ��
��
��![]() ��
��
����m=��2ʱ��S������ֵΪ1����ʱ��E������Ϊ����2��2����
����������1�����ݺ���ͼ�������㣬�ô���ϵ����ȷ�����κ����Ľ���ʽ���ɡ�
��2������BC�Ƕ�ֵ���õ���PB+PC��Сʱ����PBC���ܳ���С�����ݵ�����������Ӧ�߶εij����ɡ�
��3�����E�ĺ�����Ϊm����ʾ��E��m��2m+6����F��m��![]() ��������ʾ��EF�ij����Ӷ���ʾ��S��m�ĺ�����ϵ��Ȼ������κ�������ֵ���ɡ�
��������ʾ��EF�ij����Ӷ���ʾ��S��m�ĺ�����ϵ��Ȼ������κ�������ֵ���ɡ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABCD�У���ABC��ƽ����BE��AD�ڵ�E��
��1����֤��AE=AB��
��2����BC=8��CD=6����DE�ij��ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı�����������![]() ��
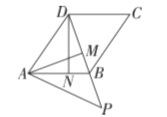
��![]() �ǵȱ������Σ�MΪ�Խ���BD������B�㣩������һ�㣬��BM�Ƶ�B��ʱ����ת60�ȵõ�BN������
�ǵȱ������Σ�MΪ�Խ���BD������B�㣩������һ�㣬��BM�Ƶ�B��ʱ����ת60�ȵõ�BN������![]()
��1����֤��![]()
��2���ٵ�M���ںδ�ʱ�� ![]() ��ֵ��С��
��ֵ��С��
�ڵ�M���ںδ�ʱ��![]() ��ֵ��С����˵������
��ֵ��С����˵������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
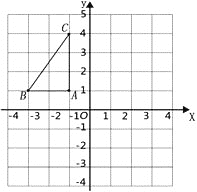
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪ ![]() ABC���������������ֱ�ΪA����1,1���� B����3,1����C����1,4����
ABC���������������ֱ�ΪA����1,1���� B����3,1����C����1,4����
�ٻ�����ABC����y��ԳƵ���A1B1C1��
�ڽ���ABC���ŵ�B˳ʱ����ת90����õ���A2BC2 �� ����ͼ�л�����A2BC2 �� ������߶�BC��ת��������ɨ���������������� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���![]() �У�����
������![]() ����
����![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ���ӳ�����ȡһ��
���ӳ�����ȡһ��![]() ��
��![]() ����
����![]() ����
����![]() �Ķ���Ϊ____________
�Ķ���Ϊ____________![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��֪��ABC�ڽ��ڡ�O,��D��OC���ӳ�����,��B����CAD��30��.
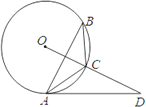
��1��AD�ǡ�O��������Ϊʲô��
��2����OD��AB,BC=5,���O�İ뾶.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ɽ��ʡƽң������Ϊ��һ���ھ���˫���¡�����ˮ��ƽң�ų��������� ��ֵ���ƻ���2019�꿪������һ��;��ƽң����վ��˫���¡���������![]() ������˼�� ˮ��ƽң�ųǵ�������+��ͨ���ںϹ���۹��ߣ��ס����������̶Ӽƻ����빤�̽��裬���üӵ���ʩ��
������˼�� ˮ��ƽң�ųǵ�������+��ͨ���ںϹ���۹��ߣ��ס����������̶Ӽƻ����빤�̽��裬���üӵ���ʩ��![]() ����ɸ���̵�
����ɸ���̵�![]() ��Ȼ���ҶӼ��룬���ӻ��蹲ͬʩ��
��Ȼ���ҶӼ��룬���ӻ��蹲ͬʩ��![]() �죬������ɸ���̣�
�죬������ɸ���̣�
��1�����Ҷӵ���ʩ������Ҫ�����������ɸ���̣�
��2�������ü�ʩ���ҼӲ�������ʩ����ʱ�䲻����![]() �죬���ҶӼ������ ��Ҫʩ�������������ɸ���̣�
�죬���ҶӼ������ ��Ҫʩ�������������ɸ���̣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB��AC����P�DZ�BC�ϵ��е㣬PD��AB��PE��AC������ֱ�Ϊ��D��E��
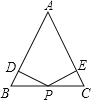
��1����֤��PD��PE��
��2����AB��6cm����BAC��30������ֱ��д��PD+PE���� ��cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ���ⳤΪ
���ⳤΪ![]() ����λ��
����λ��![]() ���������壬�ڳ�
���������壬�ڳ�![]() �Ĵ������壨��ͼ�����������桢���桢���濴���Ĵ����������ͶӰͼ������ͼ������
�Ĵ������壨��ͼ�����������桢���桢���濴���Ĵ����������ͶӰͼ������ͼ������![]() �������Σ�
��������
��1�������ͼ���У���ǰ����![]() ����������Һ�
����������Һ�![]() ��������ȡ�ߣ��ͱ��ͼ������ʱ�����桢���桢���濴����ͶӰͼ������ͼ���е�________��
��������ȡ�ߣ��ͱ��ͼ������ʱ�����桢���桢���濴����ͶӰͼ������ͼ���е�________��
��2����ͼ���У�����Ҫ����________�����������ɵ�����ͼ�Σ������濴����ͶӰͼ��ͼ�ڣ�
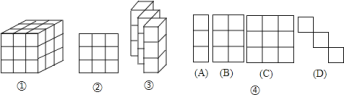
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com