
【题目】如图,ABCD中,∠ABC的平分线BE交AD于点E.
(1)求证:AE=AB;
(2)若BC=8,CD=6,求DE的长度.

 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() 中的点
中的点![]() 是
是![]() 边上的一点,过点
边上的一点,过点![]() 的反比例函数
的反比例函数![]()
![]() 与
与![]() 边交于点
边交于点![]() ,连接
,连接![]() .
.
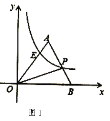
(1)如图1,若点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,且
,且![]() 的面积为5,求直线
的面积为5,求直线![]() 和反比例函数
和反比例函数![]() 的解析式;
的解析式;
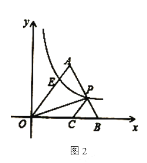
(2)如图2,若![]() ,过
,过![]() 作
作![]() ,与
,与![]() 交于点
交于点![]() ,若
,若![]() ,并且
,并且![]() 的面积为
的面积为![]() ,求反比例函数
,求反比例函数![]() 的解析式及点
的解析式及点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“黄金1号”玉米种子的价格为5元/kg.如果一次购买5kg以上的种子,超过5kg部分的种子价格打8折.
(1)购买3kg种子,需付款 元,购买6kg种子,需付款 元.
(2)设购买种子x kg,付款金额为y元,写出y与x之间的函数解析式.
(3)张大爷要购买种子5千克,李大爷要购买种子4千克,怎样购买让他们花钱最少?他们各应付款多少元?(结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,2分别是某款篮球架的实物图与示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米)(参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)

查看答案和解析>>
科目:初中数学 来源: 题型:
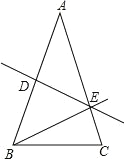
【题目】在△ABC 中,AB>BC,AB=AC,DE 是 AB 的垂直平分线,垂足为 D,交 AC 于 E.
(1)若∠ABE=40°,求∠EBC 的度数;
(2)若△ABC 的周长为 41cm,一边长为 15cm,求△BCE 的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
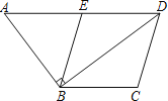
【题目】如图,四边形ABCD中,AD∥BC,AD=2BC,E为AD的中点,∠ABD=90°.
(1)求证:四边形BCDE是菱形;
(2)连接CE,若CE=6,BC=5,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF、CE,且∠FBD=35°,∠BDF=75°,下列说法:①△BDF≌CDE;②ABD和△ACD面积相等;③BF∥CE;④∠DEC=70°,其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,点A、B在x轴上、点C在y轴上,点A、B、C的坐标分别为A(![]() ,0),B(3
,0),B(3![]() ,0),C(0,5),点D在第一象限内,且∠ADB=60°,则线段CD长的最小值为( )
,0),C(0,5),点D在第一象限内,且∠ADB=60°,则线段CD长的最小值为( )
A. 2![]() B. 2
B. 2![]() ﹣2 C. 4 D. 2
﹣2 C. 4 D. 2![]() ﹣4
﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过A(-3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l与x轴交于点H.
经过A(-3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l与x轴交于点H.
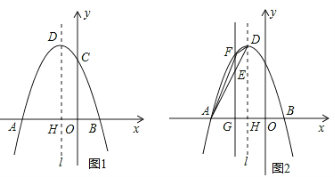
(1)求该抛物线的解析式;
(2)若点P是该抛物线对称轴l上的一个动点,求△PBC周长的最小值;
(3)如图(2),若E是线段AD上的一个动点( E与A、D不重合),过E点作平行于y轴的直线交抛物线于点F,交x轴于点G,设点E的横坐标为m,△ADF的面积为S.
①求S与m的函数关系式;
②S是否存在最大值?若存在,求出最大值及此时点E的坐标; 若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com