
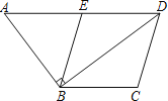
【题目】如图,四边形ABCD中,AD∥BC,AD=2BC,E为AD的中点,∠ABD=90°.
(1)求证:四边形BCDE是菱形;
(2)连接CE,若CE=6,BC=5,求四边形ABCD的面积.
【答案】(1)见解析;(2)36
【解析】
(1)根据已知条件得到四边形BCDE是平行四边形,根据直角三角形的性质得到BE=DE,于是得到结论;
(2)连接CE交BD于点O,由菱形的性质得到BD⊥CE于点O,OE=OC=![]() CE=3,根据勾股定理得到BD=
CE=3,根据勾股定理得到BD=![]() ,由三角形的面积公式即可得到结论.
,由三角形的面积公式即可得到结论.
(1)证明:∵AD=2BC,E为AD的中点,
∴DE=BC,
∵AD∥BC,
∴四边形BCDE是平行四边形,
∵∠ABD=90°,E为AD的中点,
∴BE=DE,
∴四边形BCDE是菱形;
(2)解:如图,连接CE交BD于点O,
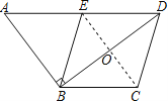
∵四边形BCDE是菱形,
∴BD⊥CE于点O,OE=OC=![]() CE=3,
CE=3,
∵E为AD的中点,
∴OE∥AB,且AB=2OE=6,
在Rt△ABD中,∠ABD=90°,AD=2BC=10,AB=6,
∴BD=![]() =
=![]() =8,
=8,
∴△ABD的面积S△ABD=![]() ×AB×BD=
×AB×BD=![]() ×6×8=24,
×6×8=24,
△BCD的面积S△BCD=![]() ×BD×OC=
×BD×OC=![]() ×8×3=12,
×8×3=12,
∴四边形ABCD的面积S=S△ABD+S△BCD=36.


科目:初中数学 来源: 题型:
【题目】小明和小亮利用三张卡片做游戏,卡片上分别写有A,B,B.这些卡片除字母外完全相同,从中随机摸出一张,记下字母后放回,充分洗匀后,再从中摸出一张,如果两次摸到卡片字母相同则小明胜,否则小亮胜,这个游戏对双方公平吗?请说明现由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线![]() 交AB,BC分别于点M,N,反比例函数
交AB,BC分别于点M,N,反比例函数![]() 的图象经过点M,N.
的图象经过点M,N.

(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC 中,∠C=90°,∠B=30°,以点 A 为圆心,任意长为半径画弧分别交 AB,AC 于点M 和 N,再分别以 M,N 为圆心,大于![]() 的长为半径画弧,两弧交于点 P,连接 AP 并延长交 BC 于点D,则下列说法中:①AD 是∠BAC 的平分线;②点 D 在线段 AB 的垂直平分线上;③S△DAC:S△ABC=1:2.正确的是( ).
的长为半径画弧,两弧交于点 P,连接 AP 并延长交 BC 于点D,则下列说法中:①AD 是∠BAC 的平分线;②点 D 在线段 AB 的垂直平分线上;③S△DAC:S△ABC=1:2.正确的是( ).
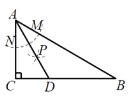
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=10,BC=12,E为DC的中点,连接BE,作AF⊥BE,垂足为F.

(1)求证:△BEC∽△ABF;
(2)求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,点D在OC的延长线上,∠B=∠CAD=30°.
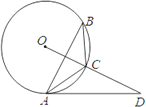
(1)AD是⊙O的切线吗?为什么?
(2)若OD⊥AB,BC=5,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com