
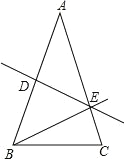
【题目】在△ABC 中,AB>BC,AB=AC,DE 是 AB 的垂直平分线,垂足为 D,交 AC 于 E.
(1)若∠ABE=40°,求∠EBC 的度数;
(2)若△ABC 的周长为 41cm,一边长为 15cm,求△BCE 的周长.
【答案】(1)30°(2)26cm
【解析】
试题(1)利用等腰三角形的性质和线段垂直平分线的性质求出∠ABC的度数,然后利用∠EBC=∠ABC﹣∠ABE计算即可;(2)利用线段垂直平分线的性质将△BCE的周长转化成AC+BC,然后利用条件计算即可.
试题解析:(1)已知AB=AC,DE是AB的垂直平分线.
∴∠ABE=∠A=40°.
又因为∠A=40°
∴∠ABC=∠ACB=70°,
∴∠EBC=∠ABC﹣∠ABE=30°.
(2)已知△ABC的周长为41cm,一边长为15cm,AB>BC
AB=15cm,
∴BC=11cm.
根据垂直平分线的性质可得BE+CE=AC,
∴△BCE周长=BE+CE+BC=26cm.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE,设∠BAD=α,∠CDE=β.
(1)如图,若点D在线段BC上,点E在线段AC上.
①如果∠ABC=60°,∠ADE=70°,那么α=°,β=°.②求α,β之间的关系式.
(2)是否存在不同于以上②中的α,β之间的关系式?若存在,请求出这个关系式(求出一个即可);若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“经过已知直线外一点作这条直线的平行线”的尺规作图过程.
已知:如图1,直线l和直线l外一点P.
求作:直线l的平行直线,使它经过点P.
作法:如图2.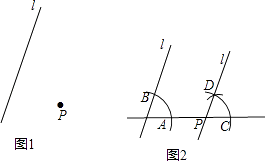
(i)过点P作直线m与直线l交于点O;
(ii)在直线m上取一点A(OA<OP),以点O为圆心,OA长为半径画弧,与直线l交于点B;
(iii)以点P为圆心,OA长为半径画弧,交直线m于点C,以点C为圆心,AB长为半径画弧,两弧交于点D;
(iv)作直线PD.
所以直线PD就是所求作的平行线.
请回答:该作图的依据是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
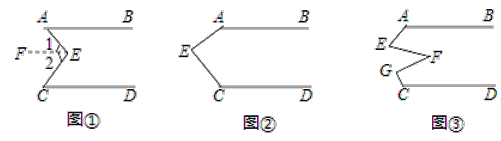
【题目】(感知)如图①,AB∥CD,点E在直线AB与CD之间,连结AE、BE,试说明∠BEE+∠DCE=∠AEC.下面给出了这道题的解题过程,请完成下面的解题过程,并填空(理由或数学式):
解:如图①,过点E作EF∥AB
∴∠BAE=∠1( )
∵AB∥CD( )
∴CD∥EF( )
∴∠2=∠DCE
∴∠BAE+∠DCE=∠1+∠2( )
∴∠BAE+∠DCE=∠AEC
(探究)当点E在如图②的位置时,其他条件不变,试说明∠AEC+∠FGC+∠DCE=360°;
(应用)点E、F、G在直线AB与CD之间,连结AE、EF、FG和CG,其他条件不变,如图③.若∠EFG=36°,则∠BAE+∠AEF+∠FGC+∠DCG= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
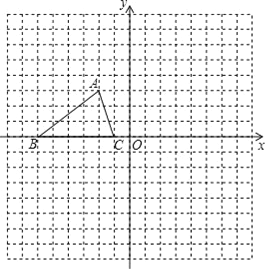
【题目】如图,已知△ABC的三个顶点的坐标分别为A(﹣2,3)、B(﹣6,0),C(﹣1,0).
(1)将△ABC向右平移5个单位,再向下平移4个单位得△A1B1C1,图中画出△A1B1C1,平移后点A的对应点A1的坐标是______.
(2)将△ABC沿x轴翻折△A2BC,图中画出△A2BC,翻折后点A对应点A2坐标是______.
(3)将△ABC向左平移2个单位,则△ABC扫过的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
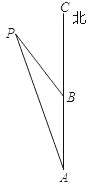
【题目】如图,一艘轮船从点 A 向正北方向航行,每小时航行 15 海里,小岛P 在轮船的北偏西 15°,3 小时后轮船航行到点 B,小岛 P 此时在轮船的北偏西 30°方向,在小岛 P 的周围 20 海里范围内有暗礁,如果轮船不改变方向继续向前航行,是否会有触礁危险?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,若点P和点P1关于y轴对称,点P1和点P2关于直线l对称,则称点P2是点P关于y轴,直线l的二次对称点.
(1)如图1,点A(﹣1,0). 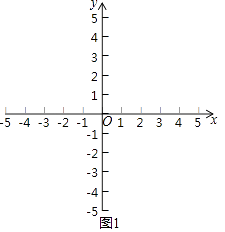
①若点B是点A关于y轴,直线l1:x=2的二次对称点,则点B的坐标为;
②若点C(﹣5,0)是点A关于y轴,直线l2:x=a的二次对称点,则a的值为;
③若点D(2,1)是点A关于y轴,直线l3的二次对称点,则直线l3的表达式为;
(2)如图2,⊙O的半径为1.若⊙O上存在点M,使得点M'是点M关于y轴,直线l4:x=b的二次对称点,且点M'在射线y= ![]() x(x≥0)上,b的取值范围是;
x(x≥0)上,b的取值范围是; 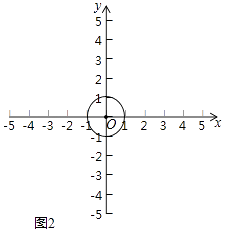
(3)E(t,0)是x轴上的动点,⊙E的半径为2,若⊙E上存在点N,使得点N'是点N关于y轴,直线l5:y= ![]() x+1的二次对称点,且点N'在y轴上,求t的取值范围.
x+1的二次对称点,且点N'在y轴上,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数![]() 的图象经过点(-3,-2).
的图象经过点(-3,-2).
(1)求这个函数表达式;
(2)判断(-5,3)是否在这个函数的图象上.
(3)点M在直线y=kx+4上且到y轴的距离是3,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。
 [来
[来
根据以上信息,解答下列问题:
(1)设租车时间为![]() 小时,租用甲公司的车所需费用为
小时,租用甲公司的车所需费用为![]() 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为![]() 元,分别求出
元,分别求出![]() ,
,![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com