
����Ŀ����ƽ��ֱ������ϵxOy�У�����P�͵�P1����y��Գƣ���P1�͵�P2����ֱ��l�Գƣ���Ƶ�P2�ǵ�P����y�ᣬֱ��l�Ķ��ζԳƵ㣮
��1����ͼ1����A����1��0���� 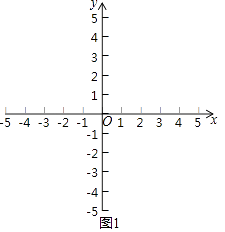
������B�ǵ�A����y�ᣬֱ��l1��x=2�Ķ��ζԳƵ㣬���B������Ϊ��
������C����5��0���ǵ�A����y�ᣬֱ��l2��x=a�Ķ��ζԳƵ㣬��a��ֵΪ��
������D��2��1���ǵ�A����y�ᣬֱ��l3�Ķ��ζԳƵ㣬��ֱ��l3�ı���ʽΪ��
��2����ͼ2����O�İ뾶Ϊ1������O�ϴ��ڵ�M��ʹ�õ�M'�ǵ�M����y�ᣬֱ��l4��x=b�Ķ��ζԳƵ㣬�ҵ�M'������y= ![]() x��x��0���ϣ�b��ȡֵ��Χ����
x��x��0���ϣ�b��ȡֵ��Χ���� 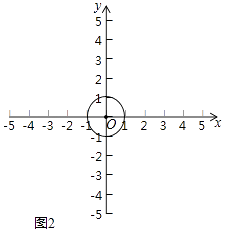
��3��E��t��0����x���ϵĶ��㣬��E�İ뾶Ϊ2������E�ϴ��ڵ�N��ʹ�õ�N'�ǵ�N����y�ᣬֱ��l5��y= ![]() x+1�Ķ��ζԳƵ㣬�ҵ�N'��y���ϣ���t��ȡֵ��Χ��
x+1�Ķ��ζԳƵ㣬�ҵ�N'��y���ϣ���t��ȡֵ��Χ��
���𰸡�
��1����3.0����-2��y=��x+2
��2���� ![]() ��b��1
��b��1
��3����ͼ6�У����E����y��ĶԳƵ�ΪE1��E1����ֱ��y= ![]() x+1�ĶԳƵ�ΪE�䣬��֪����N�ڡ�E���˶�ʱ����N���ڡ�E�����˶����ɴ˿ɼ�����E����y�����л��ཻʱ����������
x+1�ĶԳƵ�ΪE�䣬��֪����N�ڡ�E���˶�ʱ����N���ڡ�E�����˶����ɴ˿ɼ�����E����y�����л��ཻʱ����������
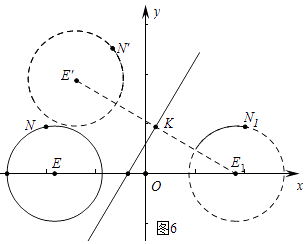
����E1E�佻ֱ��y= ![]() x+1��K����ֱ֪��E1E��Ľ���ʽΪy=��
x+1��K����ֱ֪��E1E��Ľ���ʽΪy=�� ![]() x��
x�� ![]() t��
t��
��  ���
��� 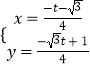 ��
��
��K�� ![]() ��
�� ![]() ����
����
��KE1=KE�䣬
��E�䣨 ![]() ��
�� ![]() ����
����
����E����y������ʱ��| ![]() |=2�����t=
|=2�����t= ![]() ��4��
��4�� ![]() +4��
+4��
��������������������t��ȡֵ��ΧΪ ![]() ��4��t��
��4��t�� ![]() +4
+4
���������⣺��1.������ͼ1�У���A����1��0������y��ĶԳƵ�A1��1��0����A1����ֱ��x=2�ĶԳƵ�B��3��0���� 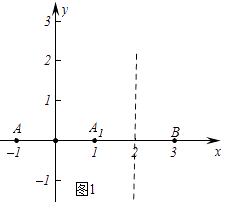
����ͼ2�У�������C����5��0����A1��1��0������A1��C����ֱ��x=a�Գƣ�
��a=��2��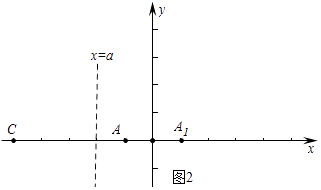
����ͼ3�У���A1��1��0����D��2��1����
��ֱ��A1D�Ľ���ʽΪy=x��1���߶�A1D���д��ߵĽ���ʽΪy=��x+2��
��ֱ��l3�Ľ���ʽΪy=��x+2��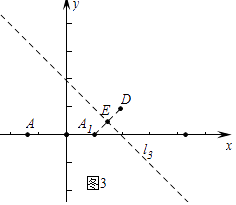
�ʴ𰸷ֱ�Ϊ��3��0����a=��2��y=��x+2��
��2.����ͼ4�У�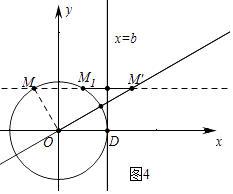
������b= ![]() MM�䣬�ɴ˿�֪����MM���ֵ���ʱ���ɵ�b�����ֵ��
MM�䣬�ɴ˿�֪����MM���ֵ���ʱ���ɵ�b�����ֵ��
��ֱ��OM��Ľ���ʽΪy= ![]() x��
x��
���MM��O=��M��OD=30�㣬
��OM=1����֪��OM��OM��ʱ��MM���ֵ������ֵΪ2��
��b�����ֵΪ1��
��ͼ5�У���֪����M��x�����������ʱ���ɵ�b����Сֵ����СֵΪ�� ![]() ��
��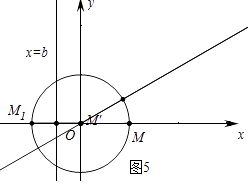
��������������������bȡֵ��ΧΪ�� ![]() ��b��1��
��b��1��
���Դ��ǩ� ![]() ��b��1��
��b��1��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У������²�����ͼ���ٷֱ���A��BΪԲ�ģ����� ![]() AB�ij�Ϊ�뾶�����������ཻ�ڵ�M��N������ֱ��MN��AC�ڵ�D������BD����CD=CB����A=35�㣬���C���ڣ� ��
AB�ij�Ϊ�뾶�����������ཻ�ڵ�M��N������ֱ��MN��AC�ڵ�D������BD����CD=CB����A=35�㣬���C���ڣ� �� 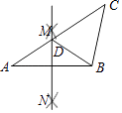
A.40��
B.50��
C.60��
D.70��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ס����������90km��A��B������ͬһ��·�Ӽس������ҵأ�A��Ħ�г���B��綯����ͼ��DE��OC�ֱ��ʾA��B�뿪�ص�·��s��km����ʱ��t��h���ĺ�����ϵ��ͼ����ͼ�����������⣮
��1��A��B���������Сʱ��B���ٶ��Ƕ��٣�
��2����B������Сʱ������������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC �У�AB��BC��AB��AC��DE �� AB �Ĵ�ֱƽ���ߣ�����Ϊ D���� AC �� E��
��1������ABE��40�㣬���EBC �Ķ�����
��2������ABC ���ܳ�Ϊ 41cm��һ�߳�Ϊ 15cm�����BCE ���ܳ���
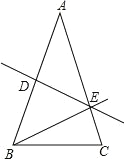
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У����κ���y=mx2����2m+1��x+m��5��ͼ����x�������������㣮
��1����m��ȡֵ��Χ��
��2����mȡ������������С�������� ��д��������κ����Ľ���ʽ��
�ڵ�n��x��1ʱ������ֵy��ȡֵ��Χ�ǩ�6��y��4��n����n��ֵ��
�۽��˶��κ���ƽ�ƣ�ʹƽ�ƺ��ͼ��ԭ��O����ƽ�ƺ��ͼ���Ӧ�ĺ�������ʽΪy=a��x��h��2+k����x��2ʱ��y��x���������С����k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ι㳡 ![]() �ı߳�Ϊ
�ı߳�Ϊ ![]() �ף��ס�������ͬѧ����Ϸ���ֱ��
�ף��ס�������ͬѧ����Ϸ���ֱ�� ![]() ��
�� ![]() ���㴦ͬʱ��������
���㴦ͬʱ�������� ![]() �ķ����ƹ㳡���ߣ����ٶ�Ϊ
�ķ����ƹ㳡���ߣ����ٶ�Ϊ ![]() ���ҵ��ٶ�Ϊ
���ҵ��ٶ�Ϊ ![]() �������˵�һ�θ��ߵ�ͬһ������ʱ( )
�������˵�һ�θ��ߵ�ͬһ������ʱ( )
A. ���ڶ��� ![]() �� B. ���ڶ���
�� B. ���ڶ��� ![]() �� C. ���ڶ���
�� C. ���ڶ���![]() �� D. ���ڶ���
�� D. ���ڶ���![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��E��F��ֱ��AB�ϣ���G���߶�CD�ϣ�ED��FG���ڵ�H����C����EFG����CED����GHD��
��1����֤��CE��GF��
��2�����жϡ�AED���D֮���������ϵ����˵�����ɣ�
��3������EHF��80������D��30�������AEM�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Rt��ABC�У���C=90������D��E�ֱ�����ABC��AC��BC�ϵĵ㣬��P��һ����.����PDA=��1����PEB=��2����DPE=�Ϧ�.
��1������P���߶�AB�ϣ���ͼ��1����ʾ�����Ϧ�=50��������1+��2=�� ���㣻
��2������P�ڱ�AB���˶�����ͼ��2����ʾ�����Ϧ�����1����2֮��Ĺ�ϵΪ���� ����
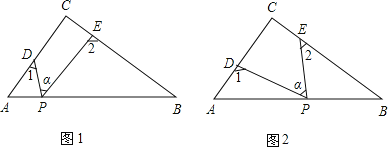
��3������P�˶�����AB���ӳ����ϣ���ͼ��3����ʾ�����Ϧ�����1����2֮���кι�ϵ�����벢˵������.
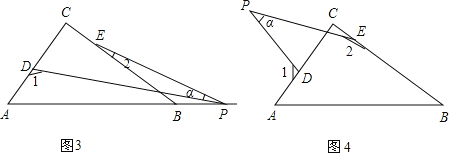
��4������P�˶�����ABC���⣬��ͼ��4����ʾ�����Ϧ�����1����2֮��Ĺ�ϵΪ������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1����ʾ����ABC�У���ABC����ACB��ƽ���߽��ڵ�O����֤����BOC=90+![]() ��A��
��A��
��ʽ1����ͼ��2����ʾ����ABC����ACD��ƽ���߽��ڵ�O����֤����BOC=![]() ��A��
��A��
��ʽ2����ͼ��3����ʾ����CBD����BCE��ƽ���߽��ڵ�O����֤����BOC=90-![]() ��A��
��A��
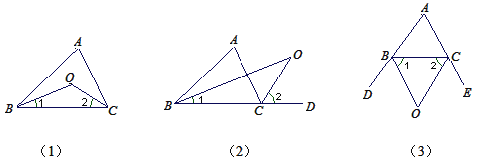
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com