
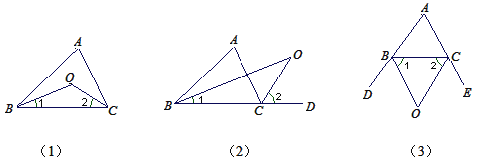
【题目】如图(1)所示,△ABC中,∠ABC,∠ACB的平分线交于点O,求证:∠BOC=90+![]() ∠A.
∠A.
变式1:如图(2)所示,∠ABC,∠ACD的平分线交于点O,求证:∠BOC=![]() ∠A.
∠A.
变式2:如图(3)所示,∠CBD,∠BCE的平分线交于点O,求证:∠BOC=90-![]() ∠A.
∠A.
【答案】见解析
【解析】
(1)先根据三角形内角和定理得到∠BOC=180°-∠OBC-∠OCB,则2∠BOC=360°-2∠OBC-2∠OCB,再根据角平分线的定义得∠ABC=2∠OBC,∠ACB=2∠OCB,则2∠BOC=360°-∠ABC-∠ACB,易得∠BOC=90°+![]() ∠A;
∠A;
变式1:根据BD为△ABC的角平分线,CD为△ABC外角∠ACE的平分线,由三角形外角性质可得;∠2=∠1+∠O,∠ACO=∠2=![]() ∠ACD=
∠ACD=![]() (∠A+∠ABC)=
(∠A+∠ABC)=![]() (∠A+2∠1) =
(∠A+2∠1) =![]() ∠A+∠1,两式联立可得 ∠1+∠O =
∠A+∠1,两式联立可得 ∠1+∠O = ![]() ∠A+∠1,即∠BOC=
∠A+∠1,即∠BOC=![]() ∠A.
∠A.
变式2:根据三角形外角平分线的性质可得∠BCO= ![]() (∠A+∠ABC)、∠OBC=
(∠A+∠ABC)、∠OBC= ![]() (∠A+∠ACB);根据三角形内角和定理可得∠BOC=90-
(∠A+∠ACB);根据三角形内角和定理可得∠BOC=90-![]() ∠A..
∠A..
(1)证明:在△BOC中,
∵∠BOC=180°-∠OBC-∠OCB,
∴2∠BOC=360°-2∠OBC-2∠OCB,
∵BO平分∠ABC,CO平分∠ACB,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∴2∠BOC=360°-(∠ABC+∠ACB),
∵∠ABC+∠ACB=180°-∠A,
∴2∠BOC=180°+∠A,
∴∠BOC=90°+![]() ∠A;
∠A;
变式1:∵BD为△ABC的角平分线,CD为△ABC外角∠ACE的平分线,
∴ ∠1= ![]() ∠ABC ∠ACO=∠2=
∠ABC ∠ACO=∠2=![]() ∠ACD
∠ACD
∵∠2、∠ACO分别是△BCO、△ABC的外角
∴∠2=∠1+∠O,∠ACO=∠2=![]() ∠ACD=
∠ACD=![]() (∠A+∠ABC)=
(∠A+∠ABC)=![]() (∠A+2∠1) =
(∠A+2∠1) =![]() ∠A+∠1,
∠A+∠1,
∴ ∠1+∠O = ![]() ∠A+∠1,
∠A+∠1,
∴∠BOC=![]() ∠A.
∠A.
变式2:∵BO、CO为△ABC中∠ABC、∠ACB的外角平分线.
∴∠BCO= ![]() (∠A+∠ABC)、∠OBC=
(∠A+∠ABC)、∠OBC= ![]() (∠A+∠ACB),
(∠A+∠ACB),
由三角形内角和定理得,∠BOC=180°-∠BCO-∠OBC,
=180°- ![]() [∠A+(∠A+∠ABC+∠ACB)],
[∠A+(∠A+∠ABC+∠ACB)],
=180°- ![]() (∠A+180°),
(∠A+180°),
=90°- ![]() ∠A;
∠A;


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,若点P和点P1关于y轴对称,点P1和点P2关于直线l对称,则称点P2是点P关于y轴,直线l的二次对称点.
(1)如图1,点A(﹣1,0). 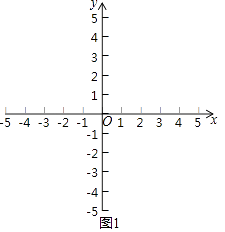
①若点B是点A关于y轴,直线l1:x=2的二次对称点,则点B的坐标为;
②若点C(﹣5,0)是点A关于y轴,直线l2:x=a的二次对称点,则a的值为;
③若点D(2,1)是点A关于y轴,直线l3的二次对称点,则直线l3的表达式为;
(2)如图2,⊙O的半径为1.若⊙O上存在点M,使得点M'是点M关于y轴,直线l4:x=b的二次对称点,且点M'在射线y= ![]() x(x≥0)上,b的取值范围是;
x(x≥0)上,b的取值范围是; 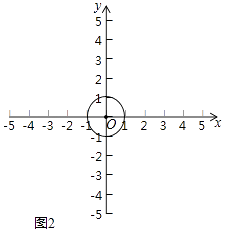
(3)E(t,0)是x轴上的动点,⊙E的半径为2,若⊙E上存在点N,使得点N'是点N关于y轴,直线l5:y= ![]() x+1的二次对称点,且点N'在y轴上,求t的取值范围.
x+1的二次对称点,且点N'在y轴上,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某电视塔周围的建筑群平面示意图,这个电视塔的位置用A表示.某人由点B出发到电视塔,他的路径表示错误的是(注:街在前,巷在后)( )
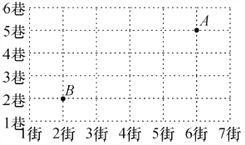
A. (2,2)→(2,5)→(5,6) B. (2,2)→(2,5)→(6,5)
C. (2,2)→(6,2)→(6,5) D. (2,2)→(2,3)→(6,3)→(6,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。
 [来
[来
根据以上信息,解答下列问题:
(1)设租车时间为![]() 小时,租用甲公司的车所需费用为
小时,租用甲公司的车所需费用为![]() 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为![]() 元,分别求出
元,分别求出![]() ,
,![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在8×8的方格纸中,△ABC的三个顶点和点P都在小方格的顶点上. 按下列要求画出图形:
(1)在图1中过点P画直线l∥BC;
(2)在图2中将△ABC平移,使点P落在平移后的△A1B1C1的内部,且△A1B1C1的三个顶点均在小方格的顶点上,请画出其中一个△A1B1C1;
(3)在图3中将△ABC平移,使△ABC的一个顶点与点P重合,请画出其中一个△A2B2C2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB交双曲线 ![]() 于A,B两点,交x轴于点C,且BC=
于A,B两点,交x轴于点C,且BC= ![]() AB,过点B作BM⊥x轴于点M,连结OA,若OM=3MC,S△OAC=8,则k的值为多少?
AB,过点B作BM⊥x轴于点M,连结OA,若OM=3MC,S△OAC=8,则k的值为多少? 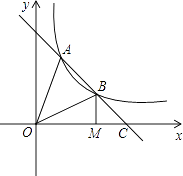
查看答案和解析>>
科目:初中数学 来源: 题型:
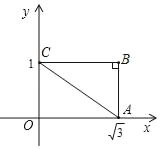
【题目】如图,在Rt△ABC中,∠B=90°,∠ACB=30°,其直角边分别与坐标轴垂直,已知顶点的坐标为A(![]() ,0),C(0,1).
,0),C(0,1).
(1)如果A关于BC对称的点是D,则点D的坐标为 ;
(2)过点B作直线m∥AC,交CD连线于E,求△BCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的三条角平分线相交于点I,过点I作DI⊥IC,交AC于点D.
(1)如图①,求证:∠AIB=∠ADI;
(2)如图②,延长BI,交外角∠ACE的平分线于点F.
①判断DI与CF的位置关系,并说明理由;
②若∠BAC=70°,求∠F的度数.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,∠ACB=45°,AD⊥BC于D,CF交AD于点F,连接BF并延长交AC于点E,∠BAD=∠FCD.求证:
(1)△ABD≌△CFD;
(2)BE⊥AC.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com