
【题目】在平面直角坐标系xOy中,二次函数y=mx2﹣(2m+1)x+m﹣5的图象与x轴有两个公共点.
(1)求m的取值范围;
(2)若m取满足条件的最小的整数, ①写出这个二次函数的解析式;
②当n≤x≤1时,函数值y的取值范围是﹣6≤y≤4﹣n,求n的值;
③将此二次函数平移,使平移后的图象经过原点O.设平移后的图象对应的函数表达式为y=a(x﹣h)2+k,当x<2时,y随x的增大而减小,求k的取值范围.
【答案】
(1)解:∵二次函数y=mx2﹣(2m+1)x+m﹣5的图象与x轴有两个公共点,
∴关于x的方程mx2﹣(2m+1)x+m﹣5=0有两个不相等的实数根,
∴ ![]() ,
,
解得:m>﹣ ![]() 且m≠0.
且m≠0.
(2)解:①∵m>﹣ ![]() 且m≠0,m取其内的最小整数,
且m≠0,m取其内的最小整数,
∴m=1,
∴二次函数的解析式为y=x2﹣3x﹣4.
②∵抛物线的对称轴为x=﹣ ![]() =
= ![]() ,1>0,
,1>0,
∴当x≤ ![]() 时,y随x的增大而减小.
时,y随x的增大而减小.
又∵n≤x≤1时,函数值y的取值范围是﹣6≤y≤4﹣n,
∴  ,解得:n=﹣2.
,解得:n=﹣2.
③根据平移的性质可知,a=1,
∵当x<2时,y随x的增大而减小,
∴h≥2.
∵平移后的图象经过原点O,
∴0=(0﹣h)2+k,即k=﹣h2,
∴k≤﹣4.
【解析】(1.)由抛物线与x轴有两个交点,可得出关于x的方程mx2﹣(2m+1)x+m﹣5=0有两个不相等的实数根,利用根的判别式△>0结合二次项系数非零,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围;(2.)①取(1)中m的最小整数,将其代入二次函数解析式中即可;②找出抛物线的对称轴为x= ![]() ,根据二次函数的性质结合“当n≤x≤1时,函数值y的取值范围是﹣6≤y≤4﹣n”,即可得出关于n的一元二次方程以及一元一次不等式,解之即可得出n的值;③根据平移的性质可得出a=1,由二次函数的性质可得出h≥2,再将(0,0)代入二次函数解析式中可得出k=﹣h2 , 进而即可得出k的取值范围.
,根据二次函数的性质结合“当n≤x≤1时,函数值y的取值范围是﹣6≤y≤4﹣n”,即可得出关于n的一元二次方程以及一元一次不等式,解之即可得出n的值;③根据平移的性质可得出a=1,由二次函数的性质可得出h≥2,再将(0,0)代入二次函数解析式中可得出k=﹣h2 , 进而即可得出k的取值范围.
【考点精析】通过灵活运用二次函数图象的平移和二次函数的最值,掌握平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a即可以解答此题.


科目:初中数学 来源: 题型:
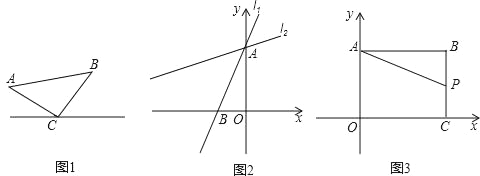
【题目】建立模型:如图1,已知△ABC,AC=BC,∠C=90°,顶点C在直线l上.
实践操作:过点A作AD⊥l于点D,过点B作BE⊥l于点E,求证:△CAD≌△BCE.
模型应用:(1)如图2,在直角坐标系中,直线l1:y=![]() x+4与y轴交于点A,与x轴交于点B,将直线l1绕着点A顺时针旋转45°得到l2.求l2的函数表达式.
x+4与y轴交于点A,与x轴交于点B,将直线l1绕着点A顺时针旋转45°得到l2.求l2的函数表达式.
(2)如图3,在直角坐标系中,点B(8,6),作BA⊥y轴于点A,作BC⊥x轴于点C,P是线段BC上的一个动点,点Q(a,2a﹣6)位于第一象限内.问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形,若能,请求出此时a的值,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
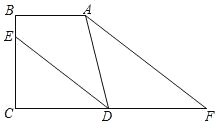
【题目】如图,AB⊥BC于点B,DC⊥BC于点C,DE平分∠ADC交BC于点E,点F为线段CD延长线上一点,∠BAF=∠EDF.
(1)求证:∠DAF=∠F;
(2)在不添加任何辅助线的情况下,请直接写出所有与∠CED互余的角.
查看答案和解析>>
科目:初中数学 来源: 题型:
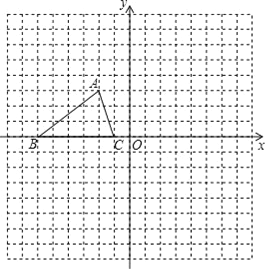
【题目】如图,已知△ABC的三个顶点的坐标分别为A(﹣2,3)、B(﹣6,0),C(﹣1,0).
(1)将△ABC向右平移5个单位,再向下平移4个单位得△A1B1C1,图中画出△A1B1C1,平移后点A的对应点A1的坐标是______.
(2)将△ABC沿x轴翻折△A2BC,图中画出△A2BC,翻折后点A对应点A2坐标是______.
(3)将△ABC向左平移2个单位,则△ABC扫过的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC度数.
小明的解题思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠APC=50°+60°=110°.
问题迁移:
(1)如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.试判断∠CPD、∠α、∠β之间有何数量关系?请说明理由;


(2)在(1)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,若点P和点P1关于y轴对称,点P1和点P2关于直线l对称,则称点P2是点P关于y轴,直线l的二次对称点.
(1)如图1,点A(﹣1,0). 
①若点B是点A关于y轴,直线l1:x=2的二次对称点,则点B的坐标为;
②若点C(﹣5,0)是点A关于y轴,直线l2:x=a的二次对称点,则a的值为;
③若点D(2,1)是点A关于y轴,直线l3的二次对称点,则直线l3的表达式为;
(2)如图2,⊙O的半径为1.若⊙O上存在点M,使得点M'是点M关于y轴,直线l4:x=b的二次对称点,且点M'在射线y= ![]() x(x≥0)上,b的取值范围是;
x(x≥0)上,b的取值范围是; 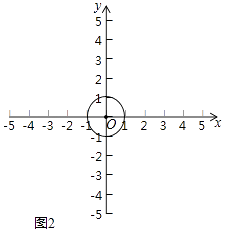
(3)E(t,0)是x轴上的动点,⊙E的半径为2,若⊙E上存在点N,使得点N'是点N关于y轴,直线l5:y= ![]() x+1的二次对称点,且点N'在y轴上,求t的取值范围.
x+1的二次对称点,且点N'在y轴上,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并完成填空.
你能比较 ![]() 和
和 ![]() 的大小吗?
的大小吗?
为了解决这个问题,先把问题一般化,比较 ![]() 和
和 ![]() (
( ![]() ,且
,且 ![]() 为整数)的大小.然后从分析
为整数)的大小.然后从分析 ![]() ,
,![]() ,
,![]()
![]() 的简单情形入手,从中发现规律,经过归纳、猜想得出结论.
的简单情形入手,从中发现规律,经过归纳、猜想得出结论.
(1)通过计算(可用计算器)比较下列(1)-(7)组两数的大小:(在横线上填上 " ![]() ""
"" ![]() “或”
“或”![]() ")
")
(1) ![]()
![]() ;(2)
;(2)![]()
![]() ;(3)
;(3)![]()
![]() ;(4)
;(4)![]()
![]() ;(5)
;(5)![]()
![]() ;(6)
;(6)![]()
![]() ;(7)
;(7)![]()
![]() ;
;
(2)归纳第(1)问的结果,可以猜想出 ![]() 和
和 ![]() 的大小关系;
的大小关系;
(3)根据以上结论,可以得出 ![]() 和
和![]() 的大小关系.
的大小关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.

(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在8×8的方格纸中,△ABC的三个顶点和点P都在小方格的顶点上. 按下列要求画出图形:
(1)在图1中过点P画直线l∥BC;
(2)在图2中将△ABC平移,使点P落在平移后的△A1B1C1的内部,且△A1B1C1的三个顶点均在小方格的顶点上,请画出其中一个△A1B1C1;
(3)在图3中将△ABC平移,使△ABC的一个顶点与点P重合,请画出其中一个△A2B2C2.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com