
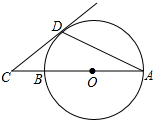
 如图所示,AB是⊙O的直径,AD是弦,∠DAB=20°,延长AB到点C,使得∠ACD=
如图所示,AB是⊙O的直径,AD是弦,∠DAB=20°,延长AB到点C,使得∠ACD= 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减/辆 | -1 | +3 | -6 | +4 | -2 | +7 | -5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=ax2+bx+3经过A(-1,0),B(3,0)两点,且交y轴于点C,对称轴与抛物线相交于点P、与直线BC相交于点M.
如图,抛物线y=ax2+bx+3经过A(-1,0),B(3,0)两点,且交y轴于点C,对称轴与抛物线相交于点P、与直线BC相交于点M.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
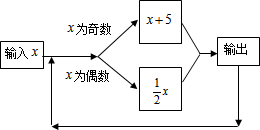 按如图所示的程序计算,若开始输入的x的值为24,我们发现第一次得到的结果为12,第2次得到的结果为6,…,请你探索第2015次得到的结果为4.
按如图所示的程序计算,若开始输入的x的值为24,我们发现第一次得到的结果为12,第2次得到的结果为6,…,请你探索第2015次得到的结果为4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,某水渠的横断面是梯形,已知其斜坡AD的坡度为1:1.2,斜坡BC的坡度为1:0.8,现测得放水前的水面宽EF为3.8米,当水闸放水后,水渠内水面宽GH为6米.则放水后水面上升的高度是( )米.
如图,某水渠的横断面是梯形,已知其斜坡AD的坡度为1:1.2,斜坡BC的坡度为1:0.8,现测得放水前的水面宽EF为3.8米,当水闸放水后,水渠内水面宽GH为6米.则放水后水面上升的高度是( )米.| A. | 1.2 | B. | 1.1 | C. | 0.8 | D. | 2.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
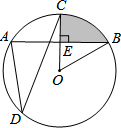 如图,A、B、C、D在⊙O上,OC⊥AB,垂足为E,∠ADC=30°,⊙O的半径为2.求:
如图,A、B、C、D在⊙O上,OC⊥AB,垂足为E,∠ADC=30°,⊙O的半径为2.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com