练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，某小区规划在一个长30m、宽20m的长方形ABCD上修建三条同样宽的通道，使其中两条与AB平行，另一条与AD平行，其余部分种花草．要使每一块花草的面积都为78m2，那么通道的宽应设计成多少m？设通道的宽为xm，由题意列得方程　　．

    　


    （30﹣2x）（20﹣x）=6×78

    考点： 由实际问题抽象出一元二次方程．

    专题： 几何图形问题．

    分析： 设道路的宽为xm，将6块草地平移为一个长方形，长为（30﹣2x）m，宽为（20﹣x）m．根据长方形面积公式即可列方程（30﹣2x）（20﹣x）=6×78．

    解答： 解：设道路的宽为xm，由题意得：

    （30﹣2x）（20﹣x）=6×78，

    故答案为：（30﹣2x）（20﹣x）=6×78．

    点评： 此题主要考查了一元二次方程的应用，掌握长方形的面积公式，求得6块草地平移为一个长方形的长和宽是解决本题的关键．

    　

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，在Rt△ABC中，∠C=90°，点P为AC边上的一点，将线段AP绕点A顺时针方向旋转（点P对应点P′），当AP旋转至AP′⊥AB时，点B、P、P′恰好在同一直线上，此时作P′E⊥AC于点E．

    （1）求证：∠CBP=∠ABP；

    （2）求证：AE=CP；

    （3）当，BP′=5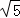时，求线段AB的长．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    直径为10cm的⊙O中，弦AB=5cm，则弦AB所对的圆周角是　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，以点P（﹣1，0）为圆心的圆，交x轴于B、C两点（B在C的左侧），交y轴于A、D两点（A在D的下方），AD=2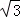，将△ABC绕点P旋转180°，得到△MCB．

    （1）求B、C两点的坐标；

    （2）请在图中画出线段MB、MC，并判断四边形ACMB的形状（不必证明），求出点M的坐标；

    （3）动直线l从与BM重合的位置开始绕点B顺时针旋转，到与BC重合时停止，设直线l与CM交点为E，点Q为BE的中点，过点E作EG⊥BC于G，连接MQ、QG．请问在旋转过程中∠MQG的大小是否变化？若不变，求出∠MQG的度数；若变化，请说明理由．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在⊙O中，OC⊥弦AB于点C，AB=4，OC=1，则OB的长是（　　）

    　 A．  B．  C．  D．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已圆的半径为r=5，圆心到直线l的距离为d，当d满足　　时，直线l与圆有公共点．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若a，b，c分别是三角形的三边，判断方程（a+b）x2+2cx+（a+b）=0的根的情况．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知⊙O的直径等于12cm，圆心O到直线l的距离为5cm，则直线l与⊙O的交点个数为   　            　．　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某学校开展课外体育活动，决定开设A：篮球、B：乒乓球、C：踢毽子、D：跑步四种活动项目．为了解学生最喜欢哪一种活动项目（每人只选取一种），随机抽取了部分学生进行调查，并将调查结果绘成如甲、乙所示的统计图，请你结合图中信息解答下列问题．

    （1）样本中最喜欢A项目的人数所占的百分比为40%，其所在扇形统计图中对应的圆心角度数是144度；

    （2）请把条形统计图补充完整；

    （3）若该校有学生1000人，请根据样本估计全校最喜欢踢毽子的学生人数约是多少？

    查看答案和解析>>

    同步练习册答案