
如图,在Rt△ABC中,∠C=90°,点P为AC边上的一点,将线段AP绕点A顺时针方向旋转(点P对应点P′),当AP旋转至AP′⊥AB时,点B、P、P′恰好在同一直线上,此时作P ′E⊥AC于点E.
′E⊥AC于点E.
(1)求证:∠CBP=∠ABP;
(2)求证:AE=CP;
(3)当 ,BP′=5
,BP′=5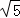 时,求线段AB的长.
时,求线段AB的长.

(1)证明:∵AP′是AP旋转得到,
∴AP=AP′,
∴∠APP′=∠AP′P,
∵∠C=90°,AP′⊥AB,
∴∠CBP+∠BPC=90°,∠ABP+∠AP′P=90°,
又∵∠BPC=∠APP′(对顶角相等),
∴∠CBP=∠ABP;
(2)证明:如图,过点P作PD⊥AB于D,
∵∠CBP=∠ABP,∠C=90°,
∴CP=DP,
∵P′E⊥AC,
∴∠EAP′+∠AP′E=90°,
又∵∠PAD+∠EAP′=90°,
∴∠PAD=∠AP′E,
在△APD和△P′AE中, ,
,
∴△APD≌△P′AE(AAS),
∴AE=DP,
∴AE=CP;
(3)解:∵ =
= ,
,
∴设CP=3k,PE=2k,
则AE=CP=3k,AP′=AP=3k+2k=5k,
在Rt△AEP′中,P′E= =4k,
=4k,
∵∠C=90°,P′E⊥AC,
∴∠CBP+∠BPC=90°,∠EP′P+∠EPP′=90°,
∵∠BPC=∠EPP′(对顶角相等),
∴∠CBP=∠EP′P,
又∵∠CBP=∠ABP,∴∠ABP=∠EP′P,
又∵∠BAP′=∠P′EP=90°,
∴△ABP′∽△EPP′,
∴ =
=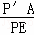 ,
,
即 =
= ,
,
解得P′A=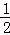 AB,
AB,
在Rt△ABP′中,AB2+P′A2=BP′2,
即AB2+ AB2=(5
AB2=(5 )2,
)2,
解得AB=10.



科目:初中数学 来源: 题型:
小明家今年种植的“红灯”樱桃喜获丰收,采摘上市20天全部销售完,小明对销售情况进行跟踪记录,并将记录情况绘成图象,日销售量y(单位:千克)与上市时间x(单位:天)的函数关系如图1所示,樱桃价格z(单位:元/千克)与上市时间x(单位:天)的函数关系式如图2所示.
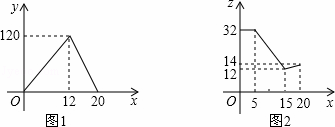
(1)观察图象,直接写出日销售量的最大值;
(2)求小明家樱桃的日销售量y与上市时间x的函数解析式;
(3)试比较第10天与第12天的销售金额哪天多?
查看答案和解析>>
科目:初中数学 来源: 题型:
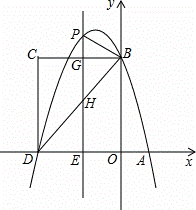
如图,在平面直角坐标系中,抛物线y=﹣ x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,某小区规划在一个长30m、宽20m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草.要使每一块花草的面积都为78m2,那么通道的宽应设计成多少m?设通道的宽为xm,由题意列得方程 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com