
【题目】已知:在平面直角坐标系中,点![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() (
(![]() 在
在![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作
作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,且
,且![]() .
.
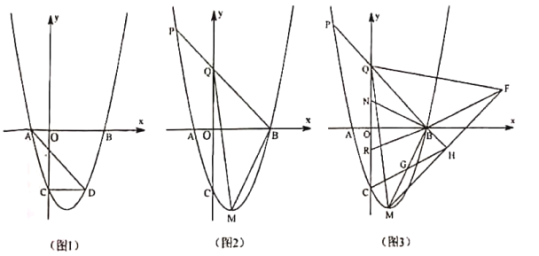
(1)如图1,求抛物线的解析式;
(2)如图2,点![]() 为第二象限抛物线上一点,
为第二象限抛物线上一点,![]() 交
交![]() 轴于点
轴于点![]() ,点
,点![]() 为抛物线的顶点,连接
为抛物线的顶点,连接![]() 、
、![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)如图3,在(2)的条件下,把![]() 沿直线
沿直线![]() 翻折使点
翻折使点![]() 落在点
落在点![]() 处,
处,![]() 与直线
与直线![]() 交于点
交于点![]() ,连接
,连接![]() 交线段
交线段![]() 于点
于点![]() ,点
,点![]() 、
、![]() 在线段
在线段![]() 上(
上(![]() 上
上![]() 下),且
下),且![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)5.
;(3)5.
【解析】
(1)由抛物线y=ax2-4ax-12a可求出AB两点坐标为(-2,0),(6,0),得OA=2,继而求出CD=4,由tan∠ADC=1可求OC=6,即得-12a=-6,a=![]() ,即可解题;
,即可解题;
(2)延长BM交y轴于S,过M作MI⊥y轴于I.设点P的坐标为(m,![]() m2-2m-6).可得OQ=-3(m+2).由直线BM可求S点坐标,由,△BMQ的面积为S=
m2-2m-6).可得OQ=-3(m+2).由直线BM可求S点坐标,由,△BMQ的面积为S=![]() ×QS(OB-MI)即可求出函数解析式;
×QS(OB-MI)即可求出函数解析式;
(3)连接BC,过点F作FT⊥x轴,过点C、G分别作x轴、y轴平行线交于X,由对称可求F(14,4),由∠OCH-∠OBR=45°,可求∠FBT+∠OBR=45°,把△BRC绕点B旋转90°至△BQZ,由QN2+CR2=NR2可得NZ=NR,证明△BNZ≌△BNR,得∠NBR=45°,由tan∠NBO=![]() ,求得ON=3,BN=3
,求得ON=3,BN=3![]() ,根据△BNR∽△CNB得BN2=NRNC,求出OR=2,即可得NR=5.
,根据△BNR∽△CNB得BN2=NRNC,求出OR=2,即可得NR=5.
(1)过点![]() 作
作![]() 于
于![]() ,
,
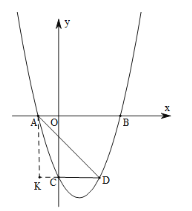
令![]() ,
,![]() ,
,
解得![]() 或6,
或6,
∴![]() ,
,
∴![]() ,
,
对称轴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴解析式为![]() ;
;
(2)延长![]() 交
交![]() 轴于
轴于![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() ,
,
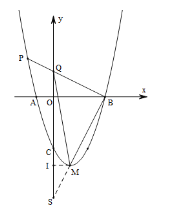
∵点P的横坐标为m,
∴点P的坐标为(m,![]() m2-2m-6).
m2-2m-6).
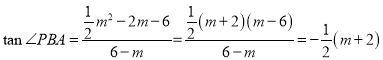
![]() ,
,
∴![]() ,
,
由![]() ,得M(2,-8),
,得M(2,-8),
设直线![]() 的解析式为:y=kx+b,
的解析式为:y=kx+b,
把M(2,-8),B(6,0)代入,得![]() ,
,
解得![]() ,
,
所以直线![]() 的解析式为
的解析式为![]() ,
,
∴![]() ,
,![]() ,
,
![]()
![]() ,
,
∴![]() ;
;
(3)连接![]() ,过点
,过点![]() 作
作![]() 轴,过点
轴,过点![]() 、
、![]() 分别作
分别作![]() 轴、
轴、![]() 轴平行线交于
轴平行线交于![]() ,
,
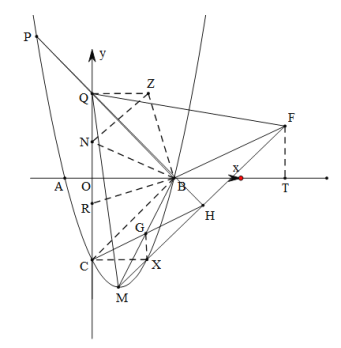
∵![]() ,
,
∴![]() ,
,
∵翻折对称得![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
由(2)知![]() ,点
,点![]() ,
,
∴![]() ,即点G坐标为(4,-4),
,即点G坐标为(4,-4),
![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
又∵![]() ,
,
∴![]() .
.
把![]() 绕点
绕点![]() 旋转
旋转![]() 至
至![]() ,
,
连接![]() ,
,
∵![]() ,
,
∴![]() ,
,
而已知![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
设![]() ,
,
![]() ,
,
∴![]() ,
,
即![]() ,
,
解得![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,连结EB,交OD于点F.
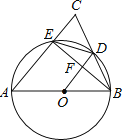
(1)求证:OD⊥BE.
(2)若DE=![]() ,AB=6,求AE的长.
,AB=6,求AE的长.
(3)若△CDE的面积是△OBF面积的![]() ,求线段BC与AC长度之间的等量关系,并说明理由.
,求线段BC与AC长度之间的等量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=2x+l与双曲线y=![]() 的一个交点为A(m,-3).
的一个交点为A(m,-3).
(1)求双曲线的表达式;
(2)过动点P(n,0)(n<0)且垂直于x轴的直线与直线y=2x+l和双曲线y=![]() 的交点分别为B,C,当点B位于点C上方时,直接写出n的取值范围.
的交点分别为B,C,当点B位于点C上方时,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
社会消费品零售总额是指批发和零售业,住宿和餐饮业以及其他行业直接售给城乡居民和社会集团的消费品零售额,在各类与消费有关的统计数据中,社会消费品零售总额是表现国内消费需求最直接的数据.
2012年,北京市全年实现社会消费品零售总额7702.8亿元,比上一年增长11.6%,2013年,全年实现社会消费品零售总额8375.1亿元,比上一年增长8.7%,2014年,全年实现社会消费品零售总额9098.1亿元,比上一年增长8.6%,2015年,全年实现社会消费品零售总额10338亿元,比上一年增长7.3%.
2016年,北京市实现市场总消费19926.2亿元,比上一年增长了8.1%,其中实现服务性消费8921.1亿元,增长10.1%;实现社会消费品零售总额11005.1亿元,比上一年增长了6.5%.
根据以上材料解答下列问题:
(1)补全统计表:
2012﹣2016年北京市社会消费品零售总额统计表
年份 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 |
社会消费品零售总额(单位:亿元) | ____ | _____ | _____ | _____ | _____ |
(2)选择适当的统计图将2012﹣2016年北京市社会消费品零售总额比上一年的增长率表示出来,并在图中表明相应数据;
(3)根据以上信息,估计2017年北京市社会消费品零售总额比上一年的增长率约为_________,你的预估理由是_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在大小为![]() 的正方形方格中,线段
的正方形方格中,线段![]() 的两端点都在单位小正方形的顶点上.
的两端点都在单位小正方形的顶点上.
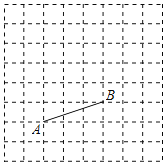
(1)在方格中画出一个![]() ,点
,点![]() 在小正方形的格点上使得
在小正方形的格点上使得![]() ,
,![]() .
.
(2)在方格中画出一个等腰![]() ,点
,点![]() 在小正方形的格点上,且使顶角为钝角,其面积等于4.
在小正方形的格点上,且使顶角为钝角,其面积等于4.
(3)在(1)(2)的条件下,连接![]() ,四边形
,四边形![]() 的面积为______个面积单位.
的面积为______个面积单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:阅读下列材料:在《北京城市总体规划(2004 年—2020 年)》中,房山区被确定为城市发展新区和生态涵养区,承担着首都经济发展、生态涵养、人口疏解和休闲度假等功能.
近年来房山区地区生产总值和财政收入均稳定增长.2011 年房山区地方生产总值是 416.0 亿元;2012 年是科学助力之年,地方生产总值 449.3 亿元,比上一年增长8.0%;2013 年房山努力在区域经济发展上取得新突破,地方生产总值是 481.8 亿元,比上年增长 7.2% ;2014 年房山区域经济稳中提质,完成地方生产总值是 519.3 亿元,比上年增长 7.8%;2015 年房山区统筹推进稳增长,地区生产总值是 554.7 亿元,比上年增长了 6.8%;2016 年经济平稳运行,地区生产总值是 593 亿元,比上年增长了 6.9%.根据以上材料解答下列问题:
(1)选择折线图或条形图将 2011 年到 2016 年的地方生产总值表示出来,并在图中标明相应数据;
(2)根据绘制的统计图中的信息,预估 2017 年房山区地方生产总值是___亿元,你的预估理由是____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形 ABCD 中,E 为直线 AB 上的动点(不与 A、B 重合),作射线 DE 并绕点 D 逆时针旋转 45°,交直线 BC 于点 F,连接 EF.
探究:当点 E 在边 AB 上,求证:EF=AE+CF.
应用:(1)当点 E 在边 AB 上,且 AD=2 时,求△BEF 的周长;
(2)当点 E 在 BA 延长线上时,判断 EF,AE,CF 三者的数量关系,并说明理由.
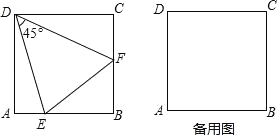
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究:
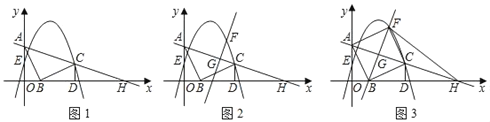
如图1,Rt△AOB的直角顶点O在坐标原点,点A在y轴正半轴上,点B在x轴正半轴上,OA=4,OB=2.将线段AB绕点B顺时针旋转90°得到线段BC,过点C作CD⊥x轴于点D,抛物线y=ax2+3x+c经过点C,与y轴交于点E(0,2),直线AC与x轴交于点H.
(1)求点C的坐标及抛物线的表达式;
(2)如图2,已知点G是线段AH上的一个动点,过点G作AH的垂线交抛物线于点F(点F在第一象限).设点G的横坐标为m.
①点G的纵坐标用含m的代数式表示为 ;
②如图3,当直线FG经过点B时,求点F的坐标,判断四边形ABCF的形状并证明结论;
③在②的前提下,连接FH,点N是坐标平面内的点,若以F,H,N为顶点的三角形与△FHC全等,请直接写出点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运算能力是一项重要的数学能力.王老师为帮助学生诊断和改进运算中的问题,对全班学生进行了三次运算测试.下面的气泡图中,描述了其中5位同学的测试成绩.(气泡圆的圆心横、纵坐标分别表示第一次和第二次测试成绩,气泡的大小表示三次成绩的平均分的高低;气泡越大平均分越高.)

①在5位同学中,有_____位同学第一次成绩比第二次成绩高;
②在甲、乙两位同学中,第三次成绩高的是_____.(填“甲”或“乙”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com