
ΓΨΧβΡΩΓΩΉέΚœ”κΧΫΨΩΘΚ
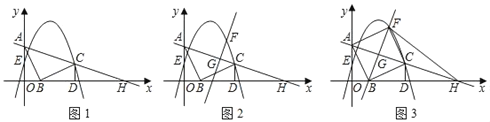
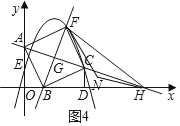
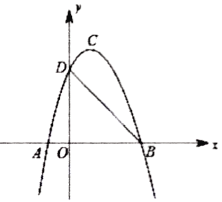
»γΆΦ1Θ§RtΓςAOBΒΡ÷±Ϋ«ΕΞΒψO‘ΎΉχ±ξ‘≠ΒψΘ§ΒψA‘Ύy÷α’ΐΑκ÷α…œΘ§ΒψB‘Ύx÷α’ΐΑκ÷α…œΘ§OAΘΫ4Θ§OBΘΫ2Θ°ΫΪœΏΕΈAB»ΤΒψBΥ≥ ±’κ–ΐΉΣ90ΓψΒΟΒΫœΏΕΈBCΘ§ΙΐΒψCΉςCDΓΆx÷α”ΎΒψDΘ§≈ΉΈοœΏyΘΫax2+3x+cΨ≠ΙΐΒψCΘ§”κy÷αΫΜ”ΎΒψE(0Θ§2)Θ§÷±œΏAC”κx÷αΫΜ”ΎΒψHΘ°
(1)«σΒψCΒΡΉχ±ξΦΑ≈ΉΈοœΏΒΡ±μ¥ο ΫΘΜ
(2)»γΆΦ2Θ§“―÷ΣΒψG «œΏΕΈAH…œΒΡ“ΜΗωΕ·ΒψΘ§ΙΐΒψGΉςAHΒΡ¥ΙœΏΫΜ≈ΉΈοœΏ”ΎΒψF(ΒψF‘ΎΒΎ“Μœσœό)Θ°…ηΒψGΒΡΚαΉχ±ξΈΣmΘ°
ΔΌΒψGΒΡΉίΉχ±ξ”ΟΚ§mΒΡ¥ζ ΐ Ϋ±μ ΨΈΣΓΓ ΓΓΘΜ
ΔΎ»γΆΦ3Θ§Β±÷±œΏFGΨ≠ΙΐΒψB ±Θ§«σΒψFΒΡΉχ±ξΘ§≈–ΕœΥΡ±Ώ–ΈABCFΒΡ–ΈΉ¥≤Δ÷ΛΟςΫα¬έΘΜ
Δέ‘ΎΔΎΒΡ«ΑΧαœ¬Θ§Ν§Ϋ”FHΘ§ΒψN «Ήχ±ξΤΫΟφΡΎΒΡΒψΘ§»τ“‘FΘ§HΘ§NΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κΓςFHC»ΪΒ»Θ§«κ÷±Ϋ”–¥≥ωΒψNΒΡΉχ±ξΘ°
ΓΨ¥πΑΗΓΩ(1)C(6Θ§2)ΘΜ≈ΉΈοœΏΫβΈω ΫΈΣyΘΫ©¹![]() x2+3x+2ΘΜ(2)ΔΌ©¹
x2+3x+2ΘΜ(2)ΔΌ©¹![]() m+4ΘΜΔΎΥΡ±Ώ–ΈABCF «’ΐΖΫ–ΈΘ§άμ”…ΦϊΫβΈωΘΜΔέΒψNΉχ±ξΈΣ(
m+4ΘΜΔΎΥΡ±Ώ–ΈABCF «’ΐΖΫ–ΈΘ§άμ”…ΦϊΫβΈωΘΜΔέΒψNΉχ±ξΈΣ(![]() Θ§
Θ§![]() )Μρ(
)Μρ(![]() Θ§
Θ§![]() )Μρ(10Θ§4)Θ°
)Μρ(10Θ§4)Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©”…œΏΕΈAB–ΐΉΣ90ΓψΒΟBC”κCDΓΆx÷αΩ…÷ΛΒΟΓςBDCΓ’ΓςAOBΘ§Ι ”–BD=OA=4Θ§CD=OB=2Θ§«σΒΟΒψCΉχ±ξΘ§ΫχΕχ”…ΒψEΓΔCΉχ±ξ”Ο¥ΐΕ®œΒ ΐΖ®Φ¥Ω…«σ≈ΉΈοœΏΫβΈω ΫΘ°
Θ®2Θ©ΔΌ”…ΒψAΓΔCΉχ±ξ”Ο¥ΐΕ®œΒ ΐΖ®«σ÷±œΏACΫβΈω ΫΘ§Α―ΒψGΚαΉχ±ξm¥ζ»κΦ¥ΒΟΒΫ”Οm±μ ΨΒψGΉίΉχ±ξΘ°
ΔΎ”…AB=BC”κBGΓΆACΩ…ΒΟAG=CGΘ§Φ¥ΒψGΈΣAC÷–ΒψΘ§ΗυΨί÷–ΒψΉχ±ξΙΪ ΫΩ…«σΒψGΉχ±ξΘ§ΫχΕχ«σ÷±œΏBGΫβΈω ΫΘ°ΝΣΝΔ÷±œΏBG”κ≈ΉΈοœΏΫβΈω ΫΫβΖΫ≥ΧΉιΦ¥«σΒΟΒψFΉχ±ξΘ°ΙΐΒψFΉςPFΓΆy÷α”ΎΒψPΘ§―”≥ΛDCΫΜPF”ΎΒψQΘ§ΗυΨίΙ¥Ι…Ε®άμ«σΒΟAB=BC=CF=AF=2![]() Θ§≈–ΕœΥΡ±Ώ–ΈABCF «Νβ–ΈΘ°‘Ό”…ΓœABC=90ΓψΦ¥÷ΛΒΟΝβ–ΈABCFΈΣ’ΐΖΫ–ΈΘ°
Θ§≈–ΕœΥΡ±Ώ–ΈABCF «Νβ–ΈΘ°‘Ό”…ΓœABC=90ΓψΦ¥÷ΛΒΟΝβ–ΈABCFΈΣ’ΐΖΫ–ΈΘ°
Δέ”…÷±œΏACΫβΈω Ϋ«σΤδ”κx÷αΫΜΒψHΒΡΉχ±ξΘ§”ΟΝΫΒψΦδΨύάκΙΪ Ϋ«σCFΓΔCHΒΡ≥ΛΘ°…ηΒψNΉχ±ξΈΣΘ®sΘ§tΘ©Θ§”ΟsΓΔtΒΡ ΫΉ”±μ ΨFN2ΓΔNH2Θ°Ζ÷άύΧ÷¬έΘΚ»τΓςFHCΓ’ΓςFHNΘ§‘ρFN=FCΘ§NH=CHΘ§Ν–ΒΟΙΊ”ΎsΓΔtΒΡΖΫ≥ΧΉιΘ§«σΫβΦ¥ΒΟΒΫΒψNΉχ±ξΘΜ»τΓςFHCΓ’ΓςHFNΘ§‘ρFN=CHΘ§NH=FCΘ§Ά§άμΩ…«σΒΟΒψNΉχ±ξΘ°
ΫβΘΚ(1)ΓΏOAΘΫ4Θ§OBΘΫ2Θ§
ΓύA(0Θ§4)Θ§B(2Θ§0)Θ§
ΓΏœΏΕΈAB»ΤΒψBΥ≥ ±’κ–ΐΉΣ90ΓψΒΟΒΫœΏΕΈBCΘ§
ΓύABΘΫBCΘ§ΓœABCΘΫ90ΓψΘ§
ΓύΓœABO+ΓœDBCΘΫΓœABO+ΓœOABΘΫ90ΓψΘ§
ΓύΓœDBCΘΫΓœOABΘ§
ΓΏCDΓΆx÷α”ΎΒψDΘ§
ΓύΓœBDCΘΫΓœAOBΘΫ90ΓψΘ§
‘ΎΓςBDC”κΓςAOB÷–Θ§
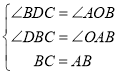 Θ§
Θ§
ΓύΓςBDCΓ’ΓςAOB(AAS)Θ§
ΓύBDΘΫOAΘΫ4Θ§CDΘΫOBΘΫ2Θ§
ΓύODΘΫOB+BDΘΫ6Θ§
ΓύC(6Θ§2)Θ§
ΓΏ≈ΉΈοœΏyΘΫax2+3x+cΨ≠ΙΐΒψCΓΔΒψE(0Θ§2)Θ§
Γύ ![]() ΫβΒΟΘΚ
ΫβΒΟΘΚ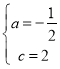 Θ§
Θ§
Γύ≈ΉΈοœΏΫβΈω ΫΈΣyΘΫ©¹![]() x2+3x+2.
x2+3x+2.
(2)ΔΌΓΏA(0Θ§4)Θ§
Γύ…η÷±œΏACΫβΈω ΫΈΣyΘΫkx+4Θ§
Α―ΒψC¥ζ»κΒΟΘΚ6k+4ΘΫ2Θ§ΫβΒΟΘΚkΘΫ©¹![]() Θ§
Θ§
Γύ÷±œΏACΘΚyΘΫ©¹![]() x+4Θ§
x+4Θ§
ΓΏΒψG‘Ύ÷±œΏAC…œΘ§ΚαΉχ±ξΈΣmΘ§
ΓύyGΘΫ©¹![]() m+4Θ§
m+4Θ§
Ι ¥πΑΗΈΣΘΚ©¹![]() m+4Θ°
m+4Θ°
ΔΎΓΏABΘΫBCΘ§BGΓΆACΘ§
ΓύAGΘΫCGΘ§Φ¥GΈΣAC÷–ΒψΘ§
ΓύG(3Θ§3)Θ§
…η÷±œΏBGΫβΈω ΫΈΣyΘΫgx+bΘ§
Γύ ![]() Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ![]() Θ§
Θ§
Γύ÷±œΏBGΘΚyΘΫ3x©¹6Θ§
ΓΏ÷±œΏBG”κ≈ΉΈοœΏΫΜΒψΈΣFΘ§«“ΒψF‘ΎΒΎ“ΜœσœόΘ§
Γύ 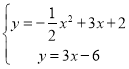 ΫβΒΟΘΚ
ΫβΒΟΘΚ 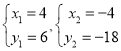 (…α»Ξ)Θ§
(…α»Ξ)Θ§
ΓύF(4Θ§6)ΘΜ
≈–ΕœΥΡ±Ώ–ΈABCF «’ΐΖΫ–ΈΘ§άμ”…»γœ¬ΘΚ
»γΆΦ1Θ§ΙΐΒψFΉςFPΓΆy÷α”ΎΒψPΘ§PF―”≥ΛœΏ”κDC―”≥ΛœΏΫΜ”ΎΒψQΘ§
 Θ§
Θ§
ΓύPFΘΫ4Θ§OPΘΫDQΘΫ6Θ§PQΘΫODΘΫ6Θ§
ΓύAPΘΫOP©¹OAΘΫ6©¹4ΘΫ2Θ§FQΘΫPQ©¹PFΘΫ6©¹4ΘΫ2Θ§CQΘΫDQ©¹CDΘΫ6©¹2ΘΫ4Θ§
ΓύAFΘΫ![]() Θ§FCΘΫ
Θ§FCΘΫ![]() Θ§
Θ§
ΓΏBCΘΫABΘΫ![]() Θ§
Θ§
ΓύABΘΫBCΘΫCFΘΫAFΘ§
ΓύΥΡ±Ώ–ΈABCF «Νβ–ΈΘ§
ΓΏΓœABCΘΫ90ΓψΘ§
ΓύΝβ–ΈABCF «’ΐΖΫ–Έ.
ΔέΓΏ÷±œΏACΘΚyΘΫ©¹![]() x+4”κx÷αΫΜ”ΎΒψHΘ§
x+4”κx÷αΫΜ”ΎΒψHΘ§
Γύ©¹![]() x+4ΘΫ0Θ§ΫβΒΟΘΚxΘΫ12Θ§
x+4ΘΫ0Θ§ΫβΒΟΘΚxΘΫ12Θ§
ΓύH(12Θ§0)Θ§
ΓύFC2ΘΫ(6©¹4)2+(2©¹6)2ΘΫ20Θ§CH2ΘΫ(12©¹6)2+(0©¹2)2ΘΫ40Θ§
…ηΒψNΉχ±ξΈΣ(sΘ§t)Θ§
ΓύFN2ΘΫ(s©¹4)2+(t©¹6)2Θ§NH2ΘΫ(s©¹12)2+(t©¹0)2Θ§
»γΆΦ2Θ§»τΓςFHCΓ’ΓςFHNΘ§‘ρFNΘΫFCΘ§NHΘΫCHΘ§
 Θ§
Θ§
Γύ ΫβΒΟΘΚ
ΫβΒΟΘΚ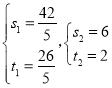 (Φ¥ΒψC)Θ§
(Φ¥ΒψC)Θ§
ΓύN![]() Θ§
Θ§
»γΆΦ3Θ§4Θ§»τΓςFHCΓ’ΓςHFNΘ§‘ρFNΘΫCHΘ§NHΘΫFCΘ§

Γύ Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ Θ§
Θ§
ΓύN![]() Θ§
Θ§
Ήέ…œΥυ ωΘ§“‘FΘ§HΘ§NΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κΓςFHC»ΪΒ» ±Θ§ΒψNΉχ±ξΈΣ(![]() Θ§
Θ§![]() )Μρ
)Μρ![]() Θ°
Θ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ’ΐΖΫ–Έ÷ΫΤ§![]() Θ§
Θ§![]() Θ§
Θ§![]() ΓΔ
ΓΔ![]() Ζ÷±π «±Ώ
Ζ÷±π «±Ώ![]() ΓΔ
ΓΔ![]() ΒΡ÷–ΒψΘ§Α―
ΒΡ÷–ΒψΘ§Α―![]() ±Ώœρ…œΖ≠’έΘ§ ΙΒψ
±Ώœρ…œΖ≠’έΘ§ ΙΒψ![]() «ΓΚΟ¬δ‘Ύ
«ΓΚΟ¬δ‘Ύ![]() …œΒΡ
…œΒΡ![]() Βψ¥ΠΘ§
Βψ¥ΠΘ§![]() ΈΣ’έΚέΘ§«“
ΈΣ’έΚέΘ§«“![]() ΫΜ
ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§‘ρ
Θ§‘ρ![]() ΒΡΟφΜΐΈΣ_____Θ°
ΒΡΟφΜΐΈΣ_____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΘΚ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§Βψ![]() ΈΣΉχ±ξ‘≠ΒψΘ§≈ΉΈοœΏ
ΈΣΉχ±ξ‘≠ΒψΘ§≈ΉΈοœΏ![]() ”κ
”κ![]() ÷αΫΜ”Ύ
÷αΫΜ”Ύ![]() ΓΔ
ΓΔ![]() Θ®
Θ®![]() ‘Ύ
‘Ύ![]() ΒΡΉσ≤ύΘ©Θ§”κ
ΒΡΉσ≤ύΘ©Θ§”κ![]() ÷αΫΜ”ΎΒψ
÷αΫΜ”ΎΒψ![]() Θ§ΙΐΒψ
Θ§ΙΐΒψ![]() Ής
Ής![]() ÷αΘ§ΫΜ≈ΉΈοœΏ”ΎΒψ
÷αΘ§ΫΜ≈ΉΈοœΏ”ΎΒψ![]() Θ§«“
Θ§«“![]() .
.
Θ®1Θ©»γΆΦ1Θ§«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©»γΆΦ2Θ§Βψ![]() ΈΣΒΎΕΰœσœό≈ΉΈοœΏ…œ“ΜΒψΘ§
ΈΣΒΎΕΰœσœό≈ΉΈοœΏ…œ“ΜΒψΘ§![]() ΫΜ
ΫΜ![]() ÷α”ΎΒψ
÷α”ΎΒψ![]() Θ§Βψ
Θ§Βψ![]() ΈΣ≈ΉΈοœΏΒΡΕΞΒψΘ§Ν§Ϋ”
ΈΣ≈ΉΈοœΏΒΡΕΞΒψΘ§Ν§Ϋ”![]() ΓΔ
ΓΔ![]() Θ§…ηΒψ
Θ§…ηΒψ![]() ΒΡΚαΉχ±ξΈΣ
ΒΡΚαΉχ±ξΈΣ![]() Θ§
Θ§![]() ΒΡΟφΜΐΈΣ
ΒΡΟφΜΐΈΣ![]() Θ§«σ
Θ§«σ![]() ”κ
”κ![]() ΒΡΚ· ΐΙΊœΒ ΫΘΜ
ΒΡΚ· ΐΙΊœΒ ΫΘΜ
Θ®3Θ©»γΆΦ3Θ§‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§Α―![]() ―Ί÷±œΏ
―Ί÷±œΏ![]() Ζ≠’έ ΙΒψ
Ζ≠’έ ΙΒψ![]() ¬δ‘ΎΒψ
¬δ‘ΎΒψ![]() ¥ΠΘ§
¥ΠΘ§![]() ”κ÷±œΏ
”κ÷±œΏ![]() ΫΜ”ΎΒψ
ΫΜ”ΎΒψ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() ΫΜœΏΕΈ
ΫΜœΏΕΈ![]() ”ΎΒψ
”ΎΒψ![]() Θ§Βψ
Θ§Βψ![]() ΓΔ
ΓΔ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() …œΘ®
…œΘ®![]() …œ
…œ![]() œ¬Θ©Θ§«“
œ¬Θ©Θ§«“![]() Θ§»τ
Θ§»τ![]() Θ§
Θ§![]() Θ§«σ
Θ§«σ![]() ΒΡ≥Λ.
ΒΡ≥Λ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
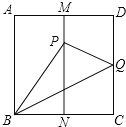
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–≈ΉΈοœΏyΘΫ©¹x2+bx+cΨ≠ΙΐΒψAΓΔBΓΔCΘ§“―÷ΣAΘ®©¹1Θ§0Θ©Θ§CΘ®0Θ§3Θ©Θ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡ±μ¥ο ΫΘΜ
Θ®2Θ©»γΆΦ1Θ§PΈΣœΏΕΈBC…œ“ΜΒψΘ§ΙΐΒψPΉςy÷αΤΫ––œΏΘ§ΫΜ≈ΉΈοœΏ”ΎΒψDΘ§Β±ΓςBCDΒΡΟφΜΐΉν¥σ ±Θ§«σΒψPΒΡΉχ±ξΘΜ
Θ®3Θ©»γΆΦ2Θ§≈ΉΈοœΏΕΞΒψΈΣEΘ§EFΓΆx÷α”ΎFΒψΘ§N «œΏΕΈEF…œ“ΜΕ·ΒψΘ§MΘ®mΘ§0Θ© «x÷α…œ“ΜΕ·ΒψΘ§»τΓœMNCΘΫ90ΓψΘ§÷±Ϋ”–¥≥ω Β ΐmΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
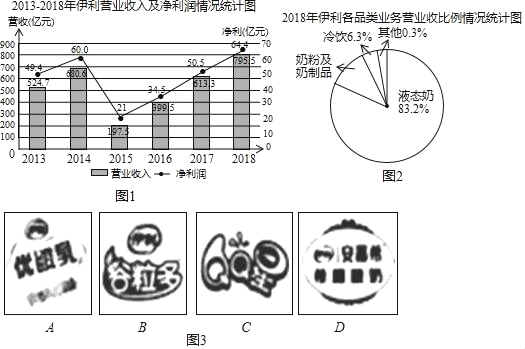
ΓΨΧβΡΩΓΩ“ΝάϊΦ·Ά≈ «÷–ΙζΙφΡΘΉν¥σΓΔ≤ζΤΖœΏΉν»ΪΒΡ»ι÷ΤΤΖΤσ“ΒΘ°ΉέΚœ ΒΦυ–ΓΉιΒΡΆ§―ߥ”Άχ…œΥ―Φ·ΒΫ»γœ¬“Μ–©“ΝάϊΦ·Ά≈ΫϋΦΗΡξΒΡ”Σ“ΒΉ¥ΩωΒΡΉ ΝœΘ§Τδ÷–ΆΦ1 «2013©¹2018Ρξ“ΝάϊΦ·Ά≈”Σ“Β ’»κΦΑΨΜάϊ»σ«ιΩωΆ≥ΦΤΆΦΘ§ΆΦ2 «2018Ρξ“ΝάϊΦ·Ά≈ΗςΤΖάύ“ΒΈώ”Σ ’±»άΐ«ιΩωΆ≥ΦΤΆΦ( ΐΨίά¥‘¥ΘΚΙΪΥΨ≤Τ±®ΓΔ÷–…Χ≤ζ“Β―–ΨΩ‘Κ)Θ°
(1)ΫβΕΝ–≈œΔΘΚ
ΉέΚœ ΒΦυ–ΓΉιΒΡΆ§―ßΫαΚœΆ≥ΦΤΆΦΧα≥ωΝΥ»γœ¬Έ ΧβΘ§«κΡψΫβ¥πΘΚ
ΔΌ2018ΡξΘ§“ΝάϊΦ·Ά≈”Σ ’ΦΑΨΜάϊ‘Ό¥ΈΥΔ–¬––“ΒΦΆ¬ΦΘ§Έ»Ψ”―«÷ό»ι“ΒΒΎ“ΜΘ°’β“ΜΡξΘ§“ΝάϊΦ·Ά≈ Βœ÷”Σ“Β ’»ΥΓΓ ΓΓ“Ύ‘ΣΘ§ΨΜάϊ»σΓΓ ΓΓ“Ύ‘ΣΘΜ
ΔΎ«σ2018Ρξ“ΝάϊΦ·Ά≈ΓΑΡΧΖέΦΑΡΧ÷ΤΤΖΓΑ“ΒΈώΒΡ”Σ“Β ’»κ(ΫαΙϊ±ΘΝτ’ϊ ΐ)ΘΜ
Δέ‘Ύ2013©¹2018’β6Ρξ÷–ΘΜ“ΝάϊΦ·Ά≈ΨΜάϊ»σ±»…œ“ΜΡξ‘ω≥ΛΕνΉνΕύΒΡ «ΓΓ ΓΓΡξΘΜΙάΦΤ2019Ρξ“ΝάϊΦ·Ά≈ΒΡΨΜάϊ»σΫΪ±»…œ“ΜΡξ‘ω≥ΛΓΓ ΓΓ“Ύ‘ΣΘ§άμ”… «ΓΓ ΓΓΘΜ
(2)ΆΊ’ΙΜνΕ·ΘΚ
»γΆΦΘ§Ά§―ßΟ« ’Φ·ΝΥ“ΝάϊΦ·Ά≈Τλœ¬ΓΑ”≈Υα»ιΓΔΙ»ΝΘΕύΓΔQQ–«Θ§Α≤ΡΜœΘΓ±ΥΡ÷÷≤ζΤΖΒΡ…Χ±ξΆΦΤ§(ΥΡ’≈ΆΦΤ§≥ΐ…Χ±ξΆΦΑΗΆβΆξ»ΪœύΆ§Θ§Ζ÷±πΦ«ΈΣAΘ§BΘ§CΘ§D)(ΦϊΆΦ3)Θ°Ά§―ßΟ«”Ο’βΥΡ’≈Ω®Τ§…ηΦΤΝΥ“ΜΗω”ΈœΖΘ§Ιφ‘ρ «ΘΚΫΪΥΡ’≈ΆΦΤ§±≥Οφ≥·…œΖ≈‘ΎΉά…œΘ§ΫΝ‘»ΚσΘ§”…ΦΉ¥”÷–ΥφΜζ≥ι»Γ“Μ’≈Θ§Φ«œ¬…Χ±ξΟϊ≥ΤΚσΖ≈ΜΊΘΜ‘Ό¥ΈΫΝ‘»ΚσΘ§”…““¥”÷–ΥφΜζ≥ι»Γ“Μ’≈Θ°»τΝΫ»Υ≥ιΒΫΒΡ…Χ±ξœύΆ§‘ρΦΉΜώ ΛΘΜΖώ‘ρΘ§““Μώ ΛΘ§’βΗωΙφ‘ρΕ‘ΦΉ““ΥΪΖΫΙΪΤΫ¬πΘΩΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§Εΰ¥ΈΚ· ΐ![]() ΒΡΆΦœσΫΜ
ΒΡΆΦœσΫΜ![]() ÷α”Ύ
÷α”Ύ![]() ΓΔ
ΓΔ![]() ΝΫΒψΘ§ΫΜ
ΝΫΒψΘ§ΫΜ![]() ÷α”ΎΒψ
÷α”ΎΒψ![]() Θ§Βψ
Θ§Βψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ§ΕΞΒψ
Θ§ΕΞΒψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() .
.
Θ®1Θ©«σΕΰ¥ΈΚ· ΐΒΡ±μ¥ο ΫΚΆ÷±œΏ![]() ΒΡ±μ¥ο ΫΘΜ
ΒΡ±μ¥ο ΫΘΜ
Θ®2Θ©Βψ![]() «÷±œΏ
«÷±œΏ![]() …œΒΡ“ΜΗωΕ·ΒψΘ§ΙΐΒψ
…œΒΡ“ΜΗωΕ·ΒψΘ§ΙΐΒψ![]() Ής
Ής![]() ÷αΒΡ¥ΙœΏΘ§ΫΜ≈ΉΈοœΏ”ΎΒψ
÷αΒΡ¥ΙœΏΘ§ΫΜ≈ΉΈοœΏ”ΎΒψ![]() Θ§Β±Βψ
Θ§Β±Βψ![]() ‘ΎΒΎ“Μœσœό ±Θ§«σœΏΕΈ
‘ΎΒΎ“Μœσœό ±Θ§«σœΏΕΈ![]() ≥ΛΕ»ΒΡΉν¥σ÷ΒΘΜ
≥ΛΕ»ΒΡΉν¥σ÷ΒΘΜ
Θ®3Θ©‘Ύ≈ΉΈοœΏ…œ¥φ‘Ύ“λ”Ύ![]() ΓΔ
ΓΔ![]() ΒΡΒψ
ΒΡΒψ![]() Θ§ Ι
Θ§ Ι![]() ÷–
÷–![]() ±Ώ…œΒΡΗΏΈΣ
±Ώ…œΒΡΗΏΈΣ![]() Θ§«κ÷±Ϋ”–¥≥ωΒψ
Θ§«κ÷±Ϋ”–¥≥ωΒψ![]() ΒΡΉχ±ξ.
ΒΡΉχ±ξ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύœ¬Ν–8ΓΝ8ΒΡΆχΗώ÷–Θ§ΚαΓΔΉίΉχ±ξΨυΈΣ’ϊΒψΒΡ ΐΫ–ΉωΗώΒψΘ§ΓςABCΒΡΕΞΒψΒΡΉχ±ξΖ÷±πΈΣAΘ®3Θ§0Θ©ΓΔBΘ®0Θ§4Θ©ΓΔCΘ®4Θ§2Θ©Θ°
Θ®1Θ©÷±Ϋ”–¥≥ωΓςABCΒΡ–ΈΉ¥ΘΜ
Θ®2Θ©“Σ«σ‘Ύœ¬ΆΦ÷–Ϋω”ΟΈόΩΧΕ»ΒΡ÷±≥ΏΉςΆΦΘΚΫΪΓςABC»ΤΒψBΡφ ±’κ–ΐΉΣΫ«Ε»2ΠΝΒΟΒΫΓςA1BC1Θ§Τδ÷–ΠΝΘΫΓœABCΘ§AΓΔCΒΡΕ‘”ΠΒψΖ÷±πΈΣA1ΓΔC1Θ§«κΡψΆξ≥…ΉςΆΦΘΜ
Θ®3Θ©‘ΎΆχΗώ÷–’““ΜΗωΗώΒψGΘ§ ΙΒΟC1GΓΆABΘ§≤Δ÷±Ϋ”–¥≥ωGΒψΒΡΉχ±ξΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
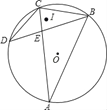
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΓςBACΈΣ‘≤OΡΎΫ”»ΐΫ«–ΈΘ§ABΘΫACΘ§DΈΣΓ―O…œ“ΜΒψΘ§Ν§Ϋ”CDΓΔBDΘ§BD”κACΫΜ”ΎΒψEΘ§«“BC2ΘΫACCE
ΔΌ«σ÷ΛΘΚΓœCDBΘΫΓœCBDΘΜ
ΔΎ»τΓœDΘΫ30ΓψΘ§«“Γ―OΒΡΑκΨΕΈΣ3+![]() Θ§IΈΣΓςBCDΡΎ–ΡΘ§«σOIΒΡ≥ΛΘ°
Θ§IΈΣΓςBCDΡΎ–ΡΘ§«σOIΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥–ΘΑΥΡξΦΕΙ≤”–8ΗωΑύΘ§241ΟϊΆ§―ßΘ§άζ Ζάœ ΠΈΣΝΥΝΥΫβ–¬÷–ΩΦΡΘ Ϋœ¬ΗΟ–ΘΑΥΡξΦΕ―ß…ζ―Γ–όάζ Ζ―ßΩΤΒΡ“βœρΘ§«κ–ΓΚλΘ§–ΓΝΝΘ§–ΓΨϋ»ΐΈΜΆ§―ßΖ÷±πΫχ––≥ι―υΒς≤ιΘ°»ΐΈΜΆ§―ßΒς≤ιΫαΙϊΖ¥άΓ»γœ¬ΘΚ

–ΓΚλΓΔ–ΓΝΝΚΆ–ΓΨϋ»ΐ»Υ÷–Θ§Ρψ»œΈΣΡΡΈΜΆ§―ßΒΡΒς≤ιΫαΙϊΫœΚΟΒΊΖ¥”≥ΝΥΗΟ–ΘΑΥΡξΦΕΆ§―ß―Γ–όάζ ΖΒΡ“βœρΘ§«κΥΒ≥ωάμ”…Θ§≤Δ”…¥ΥΙάΦΤ»ΪΡξΦΕ”–“βœρ―Γ–όάζ ΖΒΡΆ§―ßΒΡ»Υ ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com