
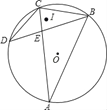
【题目】如图,已知△BAC为圆O内接三角形,AB=AC,D为⊙O上一点,连接CD、BD,BD与AC交于点E,且BC2=ACCE
①求证:∠CDB=∠CBD;
②若∠D=30°,且⊙O的半径为3+![]() ,I为△BCD内心,求OI的长.
,I为△BCD内心,求OI的长.
【答案】①证明见解析;②![]() .
.
【解析】
①先求出![]() ,然后求出△BCE和△ACB相似,根据相似三角形对应角相等可得∠A=∠CBE,再根据在同圆或等圆中,同弧所对的圆周角相等可得∠A=∠CDB,然后求出∠CDB=∠CBD;
,然后求出△BCE和△ACB相似,根据相似三角形对应角相等可得∠A=∠CBE,再根据在同圆或等圆中,同弧所对的圆周角相等可得∠A=∠CDB,然后求出∠CDB=∠CBD;
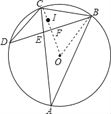
②连接OB、OC,根据在同圆或等圆中,同弧所对的圆心角等于圆周角的2倍求出∠BOC=60°,然后判定△OBC是等边三角形,再根据等腰三角形三线合一的性质以及三角形的内心的性质可得OC经过点I,设OC与BD相交于点F,然后求出CF,再根据I是三角形的内心,利用三角形的面积求出IF,然后求出CI,最后根据OI=OC﹣CI计算即可得解.
①证明:∵BC2=ACCE,
∴![]() ,
,
∠BCE=∠ACB,
∴△BCE∽△ACB,
∴∠CBD=∠A,
∵∠A=∠CDB,
∴∠CDB=∠CBD.
②解:连接OB、OC,
∵∠A=∠D=30°,
∴∠BOC=2∠A=2×30°=60°,
∵OB=OC,
∴△OBC是等边三角形,
∵CD=CB,I是△BCD的内心,
∴OC经过点I,
设OC与BD相交于点F,
则CF=BC×sin30°=![]() BC,
BC,
BF=BCcos30°=![]() BC,
BC,
所以,BD=2BF=2×![]() BC=
BC=![]() BC,
BC,
设△BCD内切圆的半径为r,
则S△BCD=![]() BDCF=
BDCF=![]() (BD+CD+BC)r,
(BD+CD+BC)r,
即![]()
![]() BC
BC![]() BC=
BC=![]() (
(![]() BC+BC+BC)r,
BC+BC+BC)r,
解得r=![]() BC=
BC=![]() BC,
BC,
即IF=![]() BC,
BC,
所以,CI=CF﹣IF=![]() BC﹣
BC﹣![]() BC=(2﹣
BC=(2﹣![]() )BC,
)BC,
OI=OC﹣CI=BC﹣(2﹣![]() )BC=(
)BC=(![]() ﹣1)BC,
﹣1)BC,
∵⊙O的半径为3+![]() ,
,
∴BC=3+![]() ,
,
∴OI=(![]() ﹣1)(3+
﹣1)(3+![]() )=3
)=3![]() +3﹣3﹣
+3﹣3﹣![]() =2
=2![]() .
.


科目:初中数学 来源: 题型:
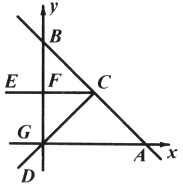
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是
是![]() 的中点,
的中点,![]() 绕点
绕点![]() 按顺时针旋转,且
按顺时针旋转,且![]() ,
,![]() 的一边
的一边![]() 交
交![]() 轴于点
轴于点![]() ,开始时另一边
,开始时另一边![]() 经过点
经过点![]() ,点
,点![]() 坐标为
坐标为![]() ,当
,当![]() 旋转过程中,射线
旋转过程中,射线![]() 与
与![]() 轴的交点由点
轴的交点由点![]() 到点
到点![]() 的过程中,则经过点
的过程中,则经过点![]() 三点的圆的圆心所经过的路径长为( )
三点的圆的圆心所经过的路径长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中放有四张分别写有数字1、2、3、4的红色卡片和三张分别写有数字1、2、3的蓝色卡片,卡片除颜色和数字外其它完全相同。
(1)从中任意抽取一张卡片,则该卡片上写有数字1的概率是;
(2)将3张蓝色卡片取出后放入另外一个不透明的盒子内,然后在两个盒子内各任意抽取一张卡片,以红色卡片上的数字作为十位数,蓝色卡片上的数字作为个位数组成一个两位数,求这个两位数大于22的概率。(请利用树状图或列表法说明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Windows2000下有一个有趣的“扫雷”游戏.如图是“扫雷”游戏的一部分,说明:图中数字2表示在以该数字为中心的周边8个方格中有2个地雷,小旗表示该方格已被探明有地雷.现在还剩下![]() 、
、![]() 、
、![]() 三个方格未被探明,其他地方为安全区(包括有数字的方格),则
三个方格未被探明,其他地方为安全区(包括有数字的方格),则![]() 、
、![]() 、
、![]() 三个方格中有地雷概率最大的方格是( )
三个方格中有地雷概率最大的方格是( )
|
|
|
|
2 | 2 | ||
|
A. A B. B C. C D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连接CD,EB.
(1)图中还有几对全等三角形,请你一一列举;
(2)求证:CF=EF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要在木里县某林场东西方向的两地之间修一条公路MN,已知点C周围200 m范围内为原始森林保护区,在MN上的点A处测得C在A的北偏东45°方向上,从A向东走600 m到达B处,测得C在点B的北偏西60°方向上.
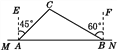
(1)MN是否穿过原始森林保护区?为什么?(参考数据: ![]() ≈1.732)
≈1.732)
(2)若修路工程顺利进行,要使修路工程比原计划提前5天完成,需将原定的工作效率提高25%,则原计划完成这项工程需要多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
第1个等式:![]()
第2个等式:![]()
第3等式:![]()
第4个等式:![]()
请解答下列问题:
(1)按以上规律写出第5个等式:a5= = .
(2)用含n的式子表示第n个等式:an= = (n为正整数).
(3)求a1+a2+a3+a4+…+a2018的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从热气球C上测得两建筑物A、B底部的俯角分别为30°和60度.如果这时气球的高度CD为90米.且点A、D、B在同一直线上,求建筑物A、B间的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com