
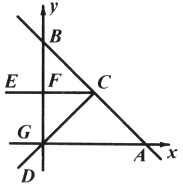
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是
是![]() 的中点,
的中点,![]() 绕点
绕点![]() 按顺时针旋转,且
按顺时针旋转,且![]() ,
,![]() 的一边
的一边![]() 交
交![]() 轴于点
轴于点![]() ,开始时另一边
,开始时另一边![]() 经过点
经过点![]() ,点
,点![]() 坐标为
坐标为![]() ,当
,当![]() 旋转过程中,射线
旋转过程中,射线![]() 与
与![]() 轴的交点由点
轴的交点由点![]() 到点
到点![]() 的过程中,则经过点
的过程中,则经过点![]() 三点的圆的圆心所经过的路径长为( )
三点的圆的圆心所经过的路径长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
此题属于半角型题目.由题意得,圆心始终在线段BC的垂直平分线上,可证△BFC是直角三角形,所以一开始经过点![]() 三点的圆的圆心在BC的中点N.开始在BC的中点N处,当射线CD经过点G时,如图,此时圆心是F′B的垂直平分线与BC的垂直平分线的交点I,在
三点的圆的圆心在BC的中点N.开始在BC的中点N处,当射线CD经过点G时,如图,此时圆心是F′B的垂直平分线与BC的垂直平分线的交点I,在 ![]() 旋转过程中,射线
旋转过程中,射线![]() 与
与![]() 轴的交点由点
轴的交点由点![]() 到点
到点![]() 的过程中,经过点
的过程中,经过点![]() 三点的圆的圆心所经过的路径长为线段NI的长.
三点的圆的圆心所经过的路径长为线段NI的长.
如图:![]() 旋转到射线
旋转到射线![]() 经过点
经过点![]() 时,表示为∠E′CD′,F′B的垂直平分线MI与BC的垂直平分线NI交于点I, MI与BN交于点 H′.
时,表示为∠E′CD′,F′B的垂直平分线MI与BC的垂直平分线NI交于点I, MI与BN交于点 H′.
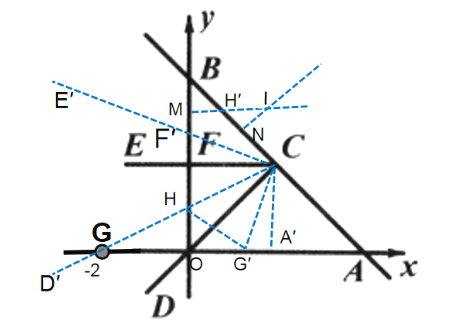
由题意得,A(4,0),B(0,4),AB的中点C(2,2),
∴∠COF=45°,又∵∠OCE=45°,∴∠CFO=90°,
过点C作CA′⊥x轴于点A′,即四边形A′OFC是边长为2的正方形.
在A′O上截取A′G′=FF′,易证Rt△CA′G′≌Rt△CFF′,
∴CF′=C G′,∠A′CG′=∠FCF′,即∠F′CG′=90°.
设A′G′=FF′=x,则O G′=2-x,F′H=H G′=x+1.
Rt△OHG′中,∵OH2+ O G′2= H G′2,即12+(2-x)2=(x+1)2,
解得:x=![]() .
.
∴F′B=4-2-![]() =
=![]() .MB=
.MB=![]() F′B =
F′B =![]() =MH′,
=MH′,
在等腰直角三角形BM H′和等腰直角三角形 H′NI中,B H′=![]()
![]() ,
,
∵BN=![]() AB=
AB=![]() ×4
×4![]() =
=![]() ,
,
∴NI=H′N=BN-B H′=![]() -
-![]()
![]() =
=![]() .
.
故选:A.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
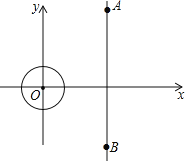
【题目】如图,在平面直角坐标系xOy中,![]() 的半径为1,A、B两点坐标分别为
的半径为1,A、B两点坐标分别为![]() 、
、![]() 已知点P是
已知点P是![]() 上的一点,点Q是线段AB上的一点,设
上的一点,点Q是线段AB上的一点,设![]() 的面积为S,当
的面积为S,当![]() 为直角三角形时,S的取值范围为______.
为直角三角形时,S的取值范围为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题6分)甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从﹣2,﹣1,3这三个数中随机抽取两个数分别记为x,y,把点M的坐标记为(x,y),若点N为(0,3),则在平面直角坐标系内直线MN经过过四象限的概率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列两则材料,回答问题,
材料一:定义直线y=ax+b与直线y=bx+a互为“互助直线”,例如,直线y=x+4与直y=4x+1互为“互助直线“
材料二:对于平面直角坐标系中的任意两点P1(x1,y1)、P2(x2,y2),P1、P2两点间的直角距离d(P1,P2)=|x1﹣x2|+|y1﹣y2|.例如:Q1(﹣3,1)、Q2(2,4)两点间的直角距离为d(Q1,Q2)=|﹣3﹣2|+|1﹣4|=8
设P0(x0,y0)为一个定点,Q(x,y)是直线y=ax+b上的动点,我们把d(P0,Q)的最小值叫做P0到直线y=ax+b的直角距离.
(1)计算S(﹣1,6),T(﹣2,3)两点间的直角距离d(S,T)= ,直线y=2x+3上的一点H(a,b)又是它的“互助直线”上的点,求点H的坐标.
(2)对于直线y=ax+b上的任意一点M(m,n),都有点N(3m,2m﹣3n)在它的“互助直线”上,试求点L(5,﹣![]() )到直线y=ax+b的直角距离.
)到直线y=ax+b的直角距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,以线段
,以线段![]() 为直径作⊙
为直径作⊙![]() ,交
,交![]() 轴的正半轴于点
轴的正半轴于点![]() ,过
,过![]() 、
、![]() 、
、![]() 三点作抛物线.
三点作抛物线.
(1)求抛物线的解析式;
(2)连结![]() ,
,![]() ,点
,点![]() 是
是![]() 延长线上一点,
延长线上一点,![]() 的角平分线
的角平分线![]() 交⊙
交⊙![]() 于点
于点![]() ,连结
,连结![]() ,在直线
,在直线![]() 上找一点
上找一点![]() ,使得
,使得![]() 的周长最小,并求出此时点
的周长最小,并求出此时点![]() 的坐标;
的坐标;
(3)在(2)的条件下,抛物线上是否存在点![]() ,使得
,使得![]() ,若存在,请直接写出点
,若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
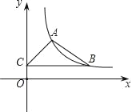
【题目】如图,在平面直角坐标系中,反比例函数![]() (x>0,k>0)的图象经过点A(1,2),B(m,n)(m>1),过点B作y轴的垂线,垂足为C.
(x>0,k>0)的图象经过点A(1,2),B(m,n)(m>1),过点B作y轴的垂线,垂足为C.
(1)求该反比例函数解析式;
(2)当△ABC面积为2时,求直线AB的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
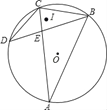
【题目】如图,已知△BAC为圆O内接三角形,AB=AC,D为⊙O上一点,连接CD、BD,BD与AC交于点E,且BC2=ACCE
①求证:∠CDB=∠CBD;
②若∠D=30°,且⊙O的半径为3+![]() ,I为△BCD内心,求OI的长.
,I为△BCD内心,求OI的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com