【题目】Windows2000下有一个有趣的“扫雷”游戏.如图是“扫雷”游戏的一部分，说明：图中数字2表示在以该数字为中心的周边8个方格中有2个地雷，小旗表示该方格已被探明有地雷.现在还剩下
、
、
三个方格未被探明，其他地方为安全区(包括有数字的方格)，则、、三个方格中有地雷概率最大的方格是( )
|
|
|
|
2 | 2 | ||
|
A. A B. B C. C D. 无法确定
怎样学好牛津英语系列答案科目：初中数学 来源： 题型：
【题目】从﹣2，﹣1，3这三个数中随机抽取两个数分别记为x，y，把点M的坐标记为（x，y），若点N为（0，3），则在平面直角坐标系内直线MN经过过四象限的概率为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在圆
中，
、
是圆的半径，点
在劣弧
上，
，
，
，连接
.
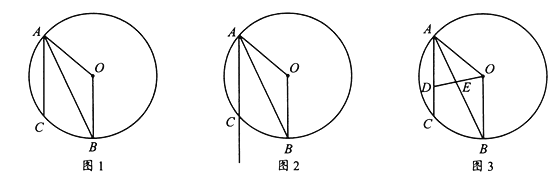
（1）如图1，试说明：平分
；
（2）如图2，点
在弦
的延长线上，连接
，如果
是直角三角形，求
的长；
（3）如图3，点
在弦上，与点
不重合，连接
与弦交于点
，设点与点的距离为
，
的面积为
，求与的函数关系式，并写出自变量的取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知
是
（
）的函数，表1中给出了几组与的对应值：
表1：
| … |
| 1 |
| 2 |
| 3 | … |
| … | 6 | 3 | 2 |
|
| 1 | … |
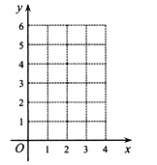
（1）以表中各对对应值为坐标，在图1的直角坐标系中描出各点，用光滑曲线顺次连接.由图像知，它是我们已经学过的哪类函数？求出函数解析式，并直接写出
的值；
（2）如果一次函数图像与（1）中图像交于
和
两点，在第一、四象限内当在什么范围时，一次函数的值小于（1）中函数的值？请直接写出答案.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线AB和抛物线的交点是A(0，-3)，B(5，9)，已知抛物线的顶点D的横坐标是2.
(1)求抛物线的解析式及顶点坐标；
(2)在
轴上是否存在一点C，与A，B组成等腰三角形？若存在，求出点C的坐标，若不存在，请说明理由；
(3)在直线AB的下方抛物线上找一点P，连接PA，PB使得△PAB的面积最大，并求出这个最大值.
查看答案和解析>>
科目：初中数学 来源： 题型：
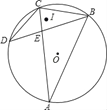
【题目】如图，已知△BAC为圆O内接三角形，AB＝AC，D为⊙O上一点，连接CD、BD，BD与AC交于点E，且BC2＝ACCE
①求证：∠CDB＝∠CBD；
②若∠D＝30°，且⊙O的半径为3+
，I为△BCD内心，求OI的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，平面直角坐标系中，矩形OABC的顶点A（﹣6，0），C（0，2
）．将矩形OABC绕点O顺时针方向旋转，使点A恰好落在OB上的点A1处，则点B的对应点B1的坐标为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，抛物线
与
轴交于
、
两点（点在点左侧），经过点的直线
：
与
轴交于点
，与抛物线的另一个交点为
，且
．
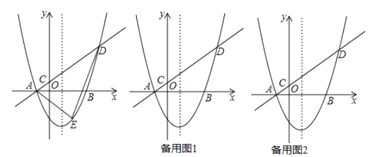
（1）直接写出点的坐标，并用含
的式子表示直线的函数表达式（其中
、
用含的式子表示）．
（2）点
为直线下方抛物线上一点，当
的面积的最大值为
时，求抛物线的函数表达式；
（3）设点
是抛物线对称轴上的一点，点
在抛物线上，以点、、、为顶点的四边形能否为矩形？若能，求出点的坐标；若不能，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
