
����Ŀ����ƽ��ֱ������ϵxOy��������y����x2+bx+c������A��B��C����֪A����1��0����C��0��3����
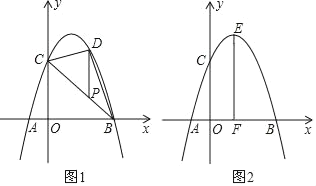
��1���������ߵı���ʽ��
��2����ͼ1��PΪ�߶�BC��һ�㣬����P��y��ƽ���ߣ����������ڵ�D������BCD��������ʱ�����P�����ꣻ
��3����ͼ2�������߶���ΪE��EF��x����F�㣬N���߶�EF��һ���㣬M��m��0����x����һ���㣬����MNC��90����ֱ��д��ʵ��m��ȡֵ��Χ��
���𰸡���1�������߽���ʽΪy����x2+2x+3��
��2����a��![]() ʱ����BDC��������ʱP��
ʱ����BDC��������ʱP��![]() ��
��![]() ����
����
��3��m��ȡֵ��ΧΪ����![]() ��m��5��
��m��5��
��������
��1����y����x2+bx+c������A��B��C��A����1��0����C��0��3�������ô���ϵ����������ô������ߵĽ���ʽ��
��2�������x2+2x+3��0����õ�B�����꣬Ȼ����ֱ��BC�Ľ���ʽΪy��kx+b�����ɴ���ϵ�����������ֱ��BC�Ľ���ʽ������P��a��3��a�������ɵ�D��a����a2+2a+3�����������PD�ij�����S��BDC��S��PDC+S��PDB�����ɵ�S��BDC����![]() ��a��
��a��![]() ��2+
��2+![]() �����ö��κ��������ʣ�������õ���BDC��������ʱ�����P�����ꣻ
�����ö��κ��������ʣ�������õ���BDC��������ʱ�����P�����ꣻ
��3��ֱ��������б���ϵ����ߵ���б�ߵ�һ���г���ϵʽm����n��![]() ��2��
��2��![]() ��Ȼ�����n��ȡֵ�õ���Сֵ��
��Ȼ�����n��ȡֵ�õ���Сֵ��
�⣺��1��������ã�![]() ��
��
��ã�![]() ��
��
�������߽���ʽΪy����x2+2x+3��
��2���x2+2x+3��0��
��x1����1��x2��3��
��B��3��0����
��ֱ��BC�Ľ���ʽΪy��kx+b����
��![]() ��
��
��ã�![]() ��
��
��ֱ��BC�Ľ���ʽΪy����x+3��
��P��a��3��a������D��a����a2+2a+3����
��PD������a2+2a+3������3��a������a2+3a��
��S��BDC��S��PDC+S��PDB
��![]() PDa+
PDa+![]() PD��3��a��
PD��3��a��
��![]() PD3
PD3
��![]() ����a2+3a��
����a2+3a��
����![]() ��a��
��a��![]() ��2+
��2+![]() ��
��
�൱a��![]() ʱ����BDC��������ʱP��
ʱ����BDC��������ʱP��![]() ��
��![]() ����
����
��3���ɣ�1����y����x2+2x+3������x��1��2+4��
��E��1��4����
��N��1��n������0��n��4��
ȡCM���е�Q��![]() ��
��![]() ����
����
�ߡ�MNC��90����
��NQ��![]() CM��
CM��
��4NQ2��CM2��
��NQ2����1��![]() ��2+��n��
��2+��n��![]() ��2��
��2��
��4[��1��![]() ��2+��n��
��2+��n��![]() ��2]��m2+9��
��2]��m2+9��
�����ã�m��n2��3n+1����m����n��![]() ��2��
��2��![]() ��
��
��0��n��4��
��n��![]() �ϣ�M��Сֵ����
�ϣ�M��Сֵ����![]() ��n��4ʱ��M��Сֵ��5��
��n��4ʱ��M��Сֵ��5��
���ϣ�m��ȡֵ��ΧΪ����![]() ��m��5��
��m��5��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����˳ij��ѧΪ�˽���꼶ѧ��������״�����Ӱ��꼶ѧ���������ȡ����ѧ���������ܲ��ԣ����Խ����ΪA��B��C��D�ĸ��ȼ������������ͳ��ͼ�е���Ϣ�ش��������⣺
��1�����γ������鹲��ȡ�˶�����ѧ����
��2������Խ��ΪC�ȼ���ѧ����������ȫ����ͼ��
��3��������ѧ���꼶����700��ѧ����������Ƹ���ѧ���꼶ѧ�������ܲ��Խ��ΪD�ȼ���ѧ���ж�������
��4����������ΪA�ȼ���2������2��Ů��������ij�ȡ2��ѧ������Ϊ��У�����˶�Ա���ص���������б�������״ͼ�ķ���������ȡ������ǡ�ö��������ĸ��ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
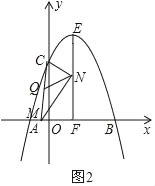
����Ŀ��ij�羰���ڵĹ�·��ͼ1��ʾ������������ѵİ������ڴ��������ظù�·�����ݵ飬;��ͣ�����֣����³�ʱ����Բ��ƣ�.��һ�����8�㷢�����Ժ�ÿ��10������һ�����ڴ�����.С����ĩ���÷羰�����棬����7:40������ڴ�����û�������ʱ�䣬���ǴӾ�����ڴ��������ظù�·����25���Ӻ����֣�����ڴ���·��![]() ���ף���ʱ��
���ף���ʱ��![]() ����)�ĺ�����ϵ��ͼ2��ʾ.
����)�ĺ�����ϵ��ͼ2��ʾ.
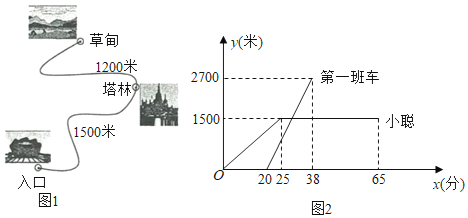
��1�����һ�����ڴ���·��![]() ���ף���ʱ��
���ף���ʱ��![]() ���֣��ĺ�������ʽ.
���֣��ĺ�������ʽ.
��2�����һ����˿ڴ��������������ʱ��.
��3��С������������40���Ӻ���������ݵ飬��СƸ�������ܹ����ϵڼ����������������ݵ飬��������������������������е��ݵ������˼����ӣ�������ÿһ��ٶȾ���ͬ��С�ϲ����ٶȲ��䣩
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ͬʱ�������꼶��ѧ���������ָ����鹲![]() �ᣬ����ۺ��ۼ����±���ʾ��
�ᣬ����ۺ��ۼ����±���ʾ��
��ѧ | ���� | |
����(Ԫ/��) |
|
|
�ۼ�(Ԫ/��) |
|
|
�蹺�����ĸ�����![]() �ᣮ
�ᣮ
![]() ��֪������깺����ѧ����������������ĸ������
��֪������깺����ѧ����������������ĸ������![]() ��ʱ��ǡ����ȥ
��ʱ��ǡ����ȥ![]() Ԫ����
Ԫ����![]() ��ֵ��
��ֵ��
![]() ��������������
��������������![]() �Ḩ�����������Ϊ
�Ḩ�����������Ϊ![]() Ԫ��
Ԫ��
����![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
�ڸ����ƻ����Ͷ��![]() Ԫ���ڹ��������ָ����飬������Ҫ�������ٲ����ĸ�����?���ɻ�õ���������Ƕ���?
Ԫ���ڹ��������ָ����飬������Ҫ�������ٲ����ĸ�����?���ɻ�õ���������Ƕ���?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
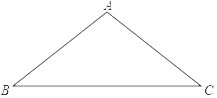
����Ŀ����ͼ����ABC��AB��AC��10��BC��16��
��1������ABC�����ԲO����Բ���ֱ����ͼ����д��������Ҫ������ͼ�ۼ���
��2����OA�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
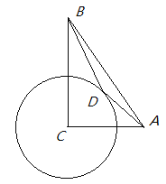
����Ŀ����ͼ����֪AC=6��BC=8��AB=10���Ե�CΪԲ�ģ�4Ϊ�뾶��Բ����D�ǡ�C�ϵ�һ�����㣬����AD��BD����AD+![]() BD����СֵΪ__________��
BD����СֵΪ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУΪ�˷ḻѧ�����������չ�����ڶ��������Ļ���Ƴ�����������ѡ�γ̣�A.�滭��B.���裻C.�ݽ���D.ʮ����.ѧУ�涨��ÿ��ѧ�������뱨���� ֻ��ѡ�����е�һ���γ�.ѧУ�������˲���ѧ����������ѡ��Ŀγ����������ͳ�ƣ� ������������������������ͳ��ͼ.����ͳ��ͼ�е���Ϣ������������⣺
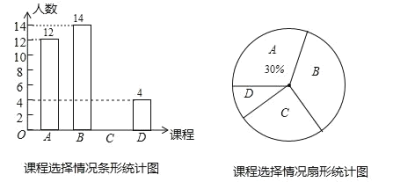
��1�����ѧУ����ѧ�������� ��C ��ռԲ�Ľ�Ϊ ��
��2��������ͳ��ͼ����������
��3�������У����1000��ѧ����������Ƹ�У��D��ѧ��Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ı���![]() Ϊ���Σ���
������![]() ��
��![]() �ϣ�����
�ϣ�����![]() ��
��![]() �غϣ�������
�غϣ�������![]() ��
��![]() ����
����![]() Ϊһ����������
Ϊһ����������![]() ��ʹ�õ�
��ʹ�õ�![]() �ڱ�
�ڱ�![]() �ϣ��������½��ۣ���
�ϣ��������½��ۣ���![]() ����
����![]() ����
����![]() ����
����![]() ����
����![]() ��������ȷ�Ľ��۵ĸ����ǣ� ��
��������ȷ�Ľ��۵ĸ����ǣ� ��
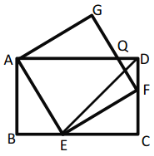
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
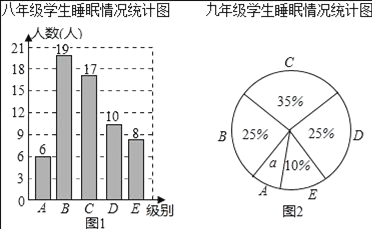
����Ŀ��Ϊ�˽�ijУ�ˡ����꼶����ѧ����˯������������ȡ�˸�У�ˡ����꼶����ѧ�����е��飬��֪��ȡ�İ��꼶����꼶��ѧ��������ͬ�����ó������õ����ݻ�����ͼ��ͳ��ͼ����
˯������ֶ��������
��� | ˯��ʱ��x��Сʱ�� |
|
|
|
|
|
|
|
|
|
|
����ͼ���ṩ����Ϣ���ش��������⣺
����ֱ��д��ͳ��ͼ��![]() ��ֵ������
��ֵ������
����˯��ʱ������6.5СʱΪ����˯�߲��㣬��Ӹ�У�ˡ����꼶�������һ��ѧ�������鵽������λѧ��˯�����ز���Ŀ����Էֱ��ж��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com