
【题目】某风景区内的公路如图1所示,景区内有免费的班车,从入口处出发,沿该公路开往草甸,途中停靠塔林(上下车时间忽略不计).第一班车上午8点发车,以后每隔10分钟有一班车从入口处发车.小聪周末到该风景区游玩,上午7:40到达入口处,因还没到班车发车时间,于是从景区入口处出发,沿该公路步行25分钟后到达塔林.离入口处的路程![]() (米)与时间
(米)与时间![]() (分)的函数关系如图2所示.
(分)的函数关系如图2所示.
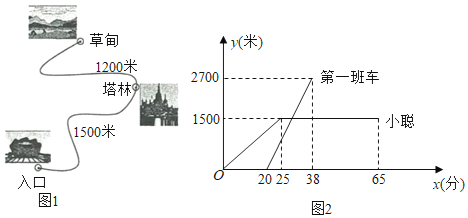
(1)求第一班车离入口处的路程![]() (米)与时间
(米)与时间![]() (分)的函数表达式.
(分)的函数表达式.
(2)求第一班车从人口处到达塔林所蓄的时间.
(3)小聪在塔林游玩40分钟后,想坐班车到草甸,则小聘聪最早能够坐上第几班车?如果他坐这班车到草甸,比他在塔林游玩结束后立即步行到草甸提早了几分钟?(假设每一班车速度均相同,小聪步行速度不变)
【答案】(1)![]() .;(2)10分钟;(3)第5班车,7分钟.
.;(2)10分钟;(3)第5班车,7分钟.
【解析】
(1)设y=kx+b,运用待定系数法求解即可;
(2)把y=1500代入(1)的结论即可;
(3)设小聪坐上了第n班车,30-25+10(n-1)≥40,解得n≥4.5,可得小聪坐上了第5班车,再根据“路程、速度与时间的关系”解答即可.
(1)解:由题意得,可设函数表达式为:![]() .
.
把![]() ,
,![]() 代入
代入![]() ,得
,得![]() ,
,
解得![]() .
.
∴第一班车离入口处的路程![]() (米)与时间
(米)与时间![]() (分)的函数表达式为
(分)的函数表达式为![]() .
.
(2)解:把![]() 代入
代入![]() ,解得
,解得![]() ,
,
![]() (分).
(分).
∴第一班车到塔林所需时间10分钟.
(3)解:设小聪坐上第![]() 班车.
班车.
![]() ,解得
,解得![]() ,
,
∴小聪最早坐上第5班车.
等班车时间为5分钟,
坐班车所需时间:![]() (分),
(分),
∴步行所需时间:![]() (分),
(分),
![]() (分).
(分).
∴小聪坐班车去草甸比他游玩结束后立即步行到达草甸提早7分钟


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象M经过
的图象M经过![]() (
(![]() ,0),
,0),![]() (2,
(2,![]() )两点且与
)两点且与![]() 轴的另一个交点为
轴的另一个交点为![]() .
.
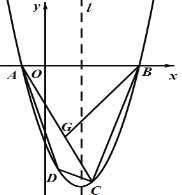
(1)求该二次函数的解析式;
(2)点![]() 是线段
是线段![]() 上的动点(点G与线段
上的动点(点G与线段![]() 的端点不重合),若△AGB∽△ABC,求点G的坐标;
的端点不重合),若△AGB∽△ABC,求点G的坐标;
(3)设抛物线的对称轴为![]() ,点
,点![]()
![]() 是抛物线上一动点,当△ACD的面积为
是抛物线上一动点,当△ACD的面积为![]() 时,点D关于
时,点D关于![]() 的对称点为E,能否在抛物线和
的对称点为E,能否在抛物线和![]() 上分别找到点P、Q,使得以点D、E、P、Q为顶点的四边形为平行四边形. 若能,求出点P的坐标;若不能,请说明理由.
上分别找到点P、Q,使得以点D、E、P、Q为顶点的四边形为平行四边形. 若能,求出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在A的正东方向有一港口B.某巡逻艇从A沿着北偏东55°方向巡逻,到达C时接到命令,立刻从C沿南偏东60°方向以20海里/小时的速度航行,从C到B航行了3小时.求A,B间的距离(结果保留整数).(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
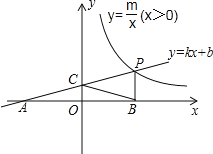
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() (x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(1)求一次函数、反比例函数的解析式;
(2)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,求出点D的坐标;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】欧几里得在《几何原本》中,记载了用图解法解方程![]() 的方法,类似地可以用折纸的方法求方程
的方法,类似地可以用折纸的方法求方程![]() 的一个正根。下面是甲、乙两位同学的做法:甲:如图1,裁一张边长为1的正方形的纸片
的一个正根。下面是甲、乙两位同学的做法:甲:如图1,裁一张边长为1的正方形的纸片![]() ,先折出
,先折出![]() 的中点
的中点![]() ,再折出线段
,再折出线段![]() ,然后通过折叠使
,然后通过折叠使![]() 落在线段
落在线段![]() 上,折出点
上,折出点![]() 的新位置
的新位置![]() ,因而
,因而![]() ,类似地,在
,类似地,在![]() 上折出点
上折出点![]() 使
使![]() 。此时,
。此时,![]() 的长度可以用来表示方程
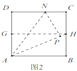
的长度可以用来表示方程![]() 的一个正根;乙:如图2,裁一张边长为1的正方形的纸片
的一个正根;乙:如图2,裁一张边长为1的正方形的纸片![]() ,先折出
,先折出![]() 的中点
的中点![]() ,再折出线段
,再折出线段![]() N,然后通过沿线段
N,然后通过沿线段![]() 折叠使
折叠使![]() 落在线段
落在线段![]() 上,折出点
上,折出点![]() 的新位置
的新位置![]() ,因而
,因而![]() 。此时,
。此时,![]() 的长度可以用来表示方程
的长度可以用来表示方程![]() 的一个正根;甲、乙两人的做法和结果( )。
的一个正根;甲、乙两人的做法和结果( )。

A.甲对,乙错B.乙对,甲错C.甲乙都对D.甲乙都错
查看答案和解析>>
科目:初中数学 来源: 题型:
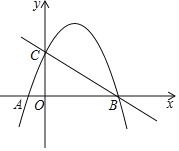
【题目】抛物线![]() 经过点A(-1,0)、B(4,0),与y轴交于点C(0,4).
经过点A(-1,0)、B(4,0),与y轴交于点C(0,4).
(1)求抛物线的表达式;
(2)点P为直线BC上方抛物线的一点,分别连接PB、PC,若直线BC恰好平分四边形COBP的面积,求P点坐标;
(3)在(2)的条件下,是否在该抛物线上存在一点Q,该抛物线对称轴上存在一点N,使得以A、P、Q、N为顶点的四边形为平行四边形?若存在,求出Q点坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
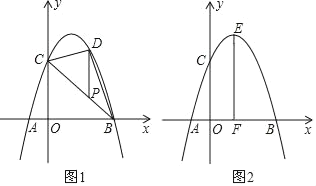
【题目】在平面直角坐标系xOy中抛物线y=﹣x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,3).
(1)求抛物线的表达式;
(2)如图1,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BCD的面积最大时,求点P的坐标;
(3)如图2,抛物线顶点为E,EF⊥x轴于F点,N是线段EF上一动点,M(m,0)是x轴上一动点,若∠MNC=90°,直接写出实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com