
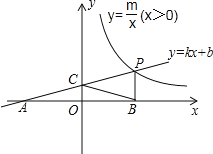
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() (x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(1)求一次函数、反比例函数的解析式;
(2)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,求出点D的坐标;如果不存在,说明理由.
【答案】(1)y=![]() x+1, y=
x+1, y=![]() ;(2)反比例函数图象上存在点D,使四边形BCPD为菱形,此时D坐标为(8,1).
;(2)反比例函数图象上存在点D,使四边形BCPD为菱形,此时D坐标为(8,1).
【解析】
(1)由AC=BC,且OC⊥AB,利用等腰三角形三线合一得到O为AB中点,求出OB的长,确定出B坐标,从而得到P点坐标,将P与A坐标代入一次函数解析式求出k与b的值,确定出一次函数解析式,将P坐标代入反比例函数的解析式求出m的值,即可确定出反比例函数的解析式;
(2)假设存在这样的D点,使四边形BCPD为菱形,根据菱形的性质得出D点的坐标.
解:(1)∵AC=BC,CO⊥AB,A(﹣4,0),
∴O为AB的中点,即OA=OB=4,
∴P(4,2),B(4,0),
将A(﹣4,0)与P(4,2)代入y=kx+b得:
![]() ,解得
,解得![]()
∴一次函数解析式为y=![]() x+1,
x+1,
将P(4,2)代入反比例解析式得:![]() ,即反比例解析式为y=
,即反比例解析式为y=![]() ;
;
(2)反比例函数图象上存在点D,使四边形BCPD为菱形,理由如下:
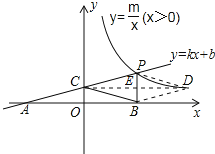
假设存在这样的D点,使四边形BCPD为菱形,如图所示,连接DC与PB交于E,
∵四边形BCPD为菱形,
∴CE=DE=4,
∴CD=8,
将x=8代入反比例函数y=![]() 得y=1,
得y=1,
∴D点的坐标为(8,1)
∴则反比例函数图象上存在点D,使四边形BCPD为菱形,此时D坐标为(8,1).


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】如图所示,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A(1,t+1),B(t-5,-1)两点.
的图象交于A(1,t+1),B(t-5,-1)两点.
(1)求一次函数和反比例函数的解析式;
(2)若点(c,p)和(n,q)是反比例函数y=![]() 图象上任意两点,且满足c=n+1时,求
图象上任意两点,且满足c=n+1时,求![]() 的值.
的值.
(3)若点M(x1,y1)和N(x2,y2)在直线AB(不与A、B重合)上,过M、N两点分别作y轴的平行线交双曲线于E、F,已知x1<-3,0<x2<1,当x1x2=-3时,判断四边形NFEM的形状.并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抚顺某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了多少名学生?
(2)求测试结果为C等级的学生数,并补全条形图;
(3)若该中学八年级共有700名学生,请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名?
(4)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解本校学生每周参加课外辅导班的情况,随机调査了部分学生一周内参加课外辅导班的学科数,并将调查结果绘制成如图1、图2所示的两幅不完整统计图(其中A:0个学科,B:1个学科,C:2个学科,D:3个学科,E:4个学科或以上),请根据统计图中的信息,解答下列问题:
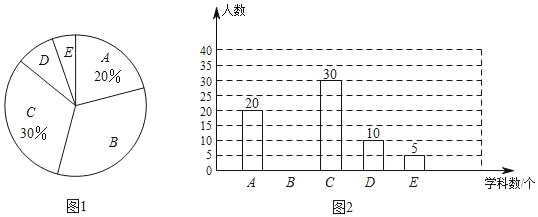
(1)请将图2的统计图补充完整;
(2)根据本次调查的数据,每周参加课外辅导班的学科数的众数是 个学科;
(3)若该校共有2000名学生,根据以上调查结果估计该校全体学生一周内参加课外辅导班在3个学科(含3个学科)以上的学生共有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
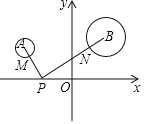
【题目】如图,平面直角坐标系中,分别以点A (﹣2,3),B(3,4)为圆心,以1、2为半径作⊙A、⊙B,M、N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值等于( )
A.![]() B.
B.![]() +3C.
+3C.![]() ﹣3D.3
﹣3D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①、图②,在给定的一张矩形纸片上作一个正方形,甲、乙两人的作法如下:
甲:以点A为圆心,AD长为半径画弧,交AB于点E,以点D为圆心,AD长为半径画弧,交CD于点F,连接EF,则四边形AEFD即为所求;
乙:作∠DAB的平分线,交CD于点M,同理作∠ADC的平分线,交AB于点N,连接MN,则四边形ADMN即为所求.


对于以上两种作法,可以做出的判定是( )
A.甲正确,乙错误B.甲、乙均正确
C.乙正确,甲错误D.甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某风景区内的公路如图1所示,景区内有免费的班车,从入口处出发,沿该公路开往草甸,途中停靠塔林(上下车时间忽略不计).第一班车上午8点发车,以后每隔10分钟有一班车从入口处发车.小聪周末到该风景区游玩,上午7:40到达入口处,因还没到班车发车时间,于是从景区入口处出发,沿该公路步行25分钟后到达塔林.离入口处的路程![]() (米)与时间
(米)与时间![]() (分)的函数关系如图2所示.
(分)的函数关系如图2所示.
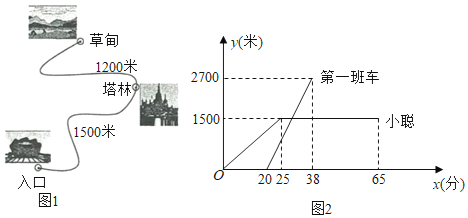
(1)求第一班车离入口处的路程![]() (米)与时间
(米)与时间![]() (分)的函数表达式.
(分)的函数表达式.
(2)求第一班车从人口处到达塔林所蓄的时间.
(3)小聪在塔林游玩40分钟后,想坐班车到草甸,则小聘聪最早能够坐上第几班车?如果他坐这班车到草甸,比他在塔林游玩结束后立即步行到草甸提早了几分钟?(假设每一班车速度均相同,小聪步行速度不变)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店同时购进九年级数学,语文两种辅导书共![]() 册,其进价和售价如下表所示:
册,其进价和售价如下表所示:
数学 | 语文 | |
进价(元/册) |
|
|
售价(元/册) |
|
|
设购进语文辅导书![]() 册.
册.
![]() 已知当该书店购进数学辅导书的数量是语文辅导书的
已知当该书店购进数学辅导书的数量是语文辅导书的![]() 倍时,恰好用去
倍时,恰好用去![]() 元,求
元,求![]() 的值.
的值.
![]() 若设该书店售完这
若设该书店售完这![]() 册辅导书的总利润为
册辅导书的总利润为![]() 元.
元.
①求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
②该书店计划最多投入![]() 元用于购买这两种辅导书,则至少要购进多少册语文辅导书?书店可获得的最大利润是多少?
元用于购买这两种辅导书,则至少要购进多少册语文辅导书?书店可获得的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形![]() 为矩形,点
为矩形,点![]() 在
在![]() 上(不与
上(不与![]() ,
,![]() 重合),连接
重合),连接![]() ,
,![]() ,以
,以![]() 为一边作正方形
为一边作正方形![]() ,使得点
,使得点![]() 在边
在边![]() 上,给出以下结论:①
上,给出以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() ;其中正确的结论的个数是( )
;其中正确的结论的个数是( )
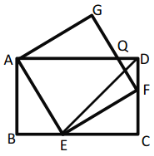
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com