
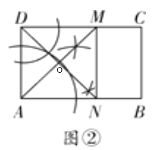
����Ŀ����ͼ�١�ͼ�ڣ��ڸ�����һ�ž���ֽƬ����һ�������Σ��ס������˵��������£�
�ף��Ե�AΪԲ�ģ�AD��Ϊ�뾶��������AB�ڵ�E���Ե�DΪԲ�ģ�AD��Ϊ�뾶��������CD�ڵ�F������EF�����ı���AEFD��Ϊ����
�ң�����DAB��ƽ���ߣ���CD�ڵ�M��ͬ������ADC��ƽ���ߣ���AB�ڵ�N������MN�����ı���ADMN��Ϊ����


�������������������������������(����)
A.����ȷ���Ҵ���B.�ס��Ҿ���ȷ
C.����ȷ���״���D.�ס��Ҿ�����
���𰸡�B
��������
��һ���ڱ���ȵľ����������ο�֪����ȷ���ɶԽ����ഹֱƽ������ȵ��ı����������ο�֪����ȷ.
�⣺�ɼ���ͼ��֪![]() ��
��![]() ��
��![]()
![]() �ı���ABCD�Ǿ���
�ı���ABCD�Ǿ���
![]()
![]() �ı���AEFD�Ǿ���
�ı���AEFD�Ǿ���
![]()
![]() �ı���AEFD�������Σ�����ȷ��
�ı���AEFD�������Σ�����ȷ��
��ͼ��AM��DN���ڵ�O��
![]() �ı���ABCD�Ǿ���
�ı���ABCD�Ǿ���
![]()
![]() �ǡ�DAB��ƽ���ߣ�
�ǡ�DAB��ƽ���ߣ�![]() �ǡ�ADC��ƽ���ߣ�
�ǡ�ADC��ƽ���ߣ�
![]() ��
��![]()
![]()
![]() ����
����![]() ��
��
![]()
![]()
ͬ����֤![]()
![]()
![]() ��AM��DN����ƽ��
��AM��DN����ƽ��
![]() �ı���AEFD�������Σ�����ȷ.
�ı���AEFD�������Σ�����ȷ.
���Լ��ҵľ���ȷ.
��ѡ��B.


 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ա�ADE����DAC��70������BAE��100����BC��DE�ཻ�ڵ�F�����DFB����Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ƽ��ֱ������ϵ�У�A(a��3)��B(b��6)��C(c��1)��a��b��c��Ϊʵ������������3b��5c����2a��18��4b��c��3a��10
(1) ��ֱ���ú�a�Ĵ���ʽ��ʾb��c
(2) ��ʵ��a�仯ʱ���ж���ABC������Ƿ����仯�������䣬����ֵ�����仯������仯��Χ
(3) ��ʵ��a�仯ʱ�����߶�AB��y���ཻ���߶�OB���߶�AC���ڵ�P����S��PAB��S��PBC����ʵ��a��ȡֵ��Χ.


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������е�����������![]() ��
��![]() ��
��![]() �����������������²��������κ����ڵ���������������ߵ�����ȥ�ұߵ�����������֮��д����������֮�䣬���ɲ���һ������������2,7,-5,-13,8����Ϊ��һ�β��������ڶ���ͬ���IJ������ֲ���һ������������2,-5,7,12,-5,8,-13,-21,8���������μ���������ȥ��ֱ����
�����������������²��������κ����ڵ���������������ߵ�����ȥ�ұߵ�����������֮��д����������֮�䣬���ɲ���һ������������2,7,-5,-13,8����Ϊ��һ�β��������ڶ���ͬ���IJ������ֲ���һ������������2,-5,7,12,-5,8,-13,-21,8���������μ���������ȥ��ֱ����![]() �β�����ֹͣ���������
�β�����ֹͣ���������![]() �β������������������и����ĺ�Ϊ_____��
�β������������������и����ĺ�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���������ϵ�A����B��Ӧ�����ֱ���6����6����DCE��90������C���O�غϣ���D��������������ϣ�
��1����ͼ1����CFƽ�֡�ACE�����AOF���� ���ȣ���A���B�ľ���=��
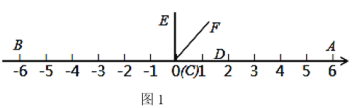
��2����ͼ2������DCE�����������������ƽ��t��0��t��3������λ�����Ƶ㶥��C��ʱ����ת30t�ȣ���CFƽ�֡�ACE����ʱ�ǡ�DCF������

����t��1ʱ�������� ������B���C�ľ���=��
��������BCE������������ϵ����˵�����ɣ�
��3����ͼ3����ʼ��D1C1E1���DCE�غϣ�����DCE�����������������ƽ��t��0![]() t
t![]() 3������λ�����Ƶ㶥��C��ʱ����ת30t�ȣ���CFƽ�֡�ACE����ʱ�ǡ�DCF���������ͬʱ������D1C1E1������ĸ���������ƽ��t��0
3������λ�����Ƶ㶥��C��ʱ����ת30t�ȣ���CFƽ�֡�ACE����ʱ�ǡ�DCF���������ͬʱ������D1C1E1������ĸ���������ƽ��t��0![]() t
t![]() 3������λ�����Ƶ㶥��C1˳ʱ����ת30t�ȣ���C1F1ƽ�֡�AC1E1���ǡ�D1C1F1������������������|������|��20������t��ֵ��
3������λ�����Ƶ㶥��C1˳ʱ����ת30t�ȣ���C1F1ƽ�֡�AC1E1���ǡ�D1C1F1������������������|������|��20������t��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ҹ������¹ڷ������飬ijʡ�ڽ����� C��D ��֪ A��B ���зֱ����Ԯ���� 200�ֺ� 300 �ֵ���Ϣ������������֧Ԯ����֪ C ���о�Ԯ���� 240 �֣�D ���о�Ԯ���� 260 �֣��ֽ���Щ��Ԯ����ȫ������ A��B ���У���֪�� C ������ A��B ���еķ��÷ֱ�Ϊÿ�� 20 Ԫ�� 25 Ԫ����D �������� A��B ���еķ��÷ֱ�Ϊÿ�� 15 Ԫ�� 30 Ԫ����� C ������ A �еľ�Ԯ����Ϊ x �֣�
��1�� ��������
A | B | �ϼƣ��֣� | |
C | x | _____ | 240 |
D | _____ | _____ | 260 |
�ܼƣ��֣� | 200 | 300 | 500 |
��2���� C��D ���е����˷�Ϊ W Ԫ���� W �� x ֮��ĺ�����ϵʽΪ_________�������Ա��� x��ȡֵ��Χ��________��
��3���������ޣ��� C �е� B �е�·���õ��˸��ƣ�����������ʱ�䣬�˷�ÿ�ּ��� n Ԫ��n��10��������·���˷Ѳ��䣬�� C��D ���е����˷ѵ���Сֵ��С�� 7920 Ԫ���� n ��ȡֵ��Χ��______________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
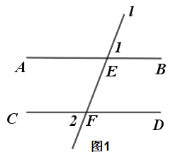
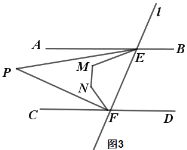
����Ŀ����֪��ֱ��l�ֱ�AB��CD��E��F���㣬��AB��CD��
��1�� ˵������1=��2��
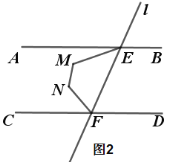
��2�� ��ͼ2����M��N��AB��CD֮�䣬����ֱ��l��࣬����EMN+��FNM=260����
������AEM+��CFN�Ķ�����
����ͼ3����EPƽ����AEM��FPƽ����CFN������P�Ķ�����
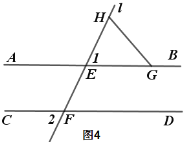
��3�� ��ͼ4����2=80������G������EB�ϣ���H��AB�Ϸ���ֱ��l�ϣ���Q��ƽ����һ�㣬����QG��QH������AGQ=18������FHQ=24����ֱ��д����GQH�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=��x2+2x+3��x�ύ��A��B���㣨��A�ڵ�B����ߣ�����y�ύ�ڵ�C������BC��
��1����A��B��C��������ꣻ
��2������PΪ�߶�BC��һ�㣨����B��C�غϣ���PM��y�ᣬ��PM���������ڵ�M����x���ڵ�N������BCM��������ʱ�����BPN���ܳ���
��3���ڣ�2���������£�����BCM��������ʱ���������ߵĶԳ����ϴ���һ��Q��ʹ�á�CNQΪֱ�������Σ����Q�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������� 1������
2����һ�κ���y=kx+b������A��3��4����B��4��5��������һ�κ����Ľ���ʽ��
��1���Ȼ�������ֵ�� ![]() �£�2+
�£�2+ ![]() ��
��
��2����һ�κ���y=kx+b������A��3��4����B��4��5��������һ�κ����Ľ���ʽ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com