
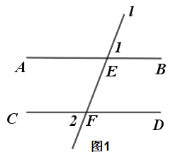
【题目】已知:直线l分别交AB、CD与E、F两点,且AB∥CD.
(1) 说明:∠1=∠2;
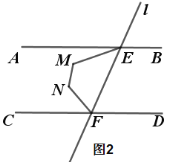
(2) 如图2,点M、N在AB、CD之间,且在直线l左侧,若∠EMN+∠FNM=260°,
①求:∠AEM+∠CFN的度数;
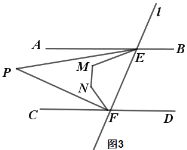
②如图3,若EP平分∠AEM,FP平分∠CFN,求∠P的度数;
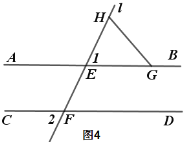
(3) 如图4,∠2=80°,点G在射线EB上,点H在AB上方的直线l上,点Q是平面内一点,连接QG、QH,若∠AGQ=18°,∠FHQ=24°,直接写出∠GQH的度数.
【答案】(1)理由见解析;(2)①80°,②40°;(3)38°、74°、86°、122°.
【解析】
(1)根据平行线的性质及对顶角的性质即可得证;
(2)①过拐点作AB的平行线,根据平行线的性质推理即可得到答案;
②过点P作AB的平行线,根据平行线的性质及角平分线的定义求得角的度数;
(3)分情况讨论,画出图形,根据三角形的内角和与外角的性质分别求出答案即可.
(1)![]()
![]() ,
,
![]()
![]() ;
;
(2)①分别过点M,N作直线GH,IJ与AB平行,则![]() ,如图:
,如图:
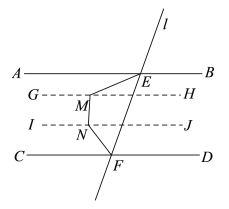
![]() ,
,![]() ,
,![]() ,
,
![]() ;
;
②过点P作AB的平行线,
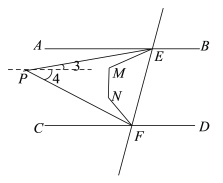
根据平行线的性质可得:![]() ,
,![]() ,
,
∵EP平分∠AEM,FP平分∠CFN,
∴![]() ,
,
即![]() ;
;
(3)分四种情况进行讨论:
由已知条件可得![]() ,
,
①如图:
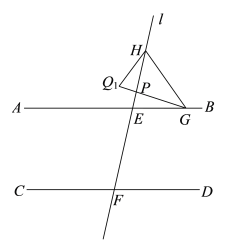
![]()
![]()
![]()
②如图:
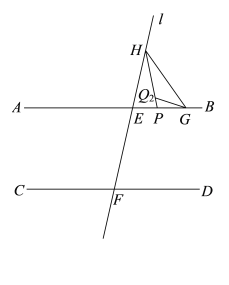
![]() ,
,
![]() ;
;
③如图:
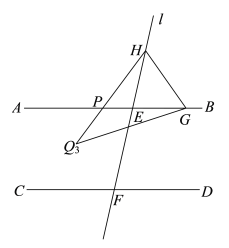
![]() ,
,
![]() ;
;
④如图:
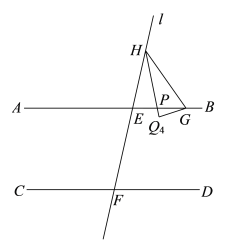
![]() ,
,
![]() ;
;
综上所述,∠GQH的度数为38°、74°、86°、122°.


科目:初中数学 来源: 题型:
【题目】如图1,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字1,2,3,4.如图2,正方形ABCD顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.
如:若从圈A起跳,第一次掷得3,就顺时针连续跳3个边长,落到圈D;若第二次掷得2,就从D开始顺时针连续跳2个边长,落到圈B;…
设游戏者从圈A起跳.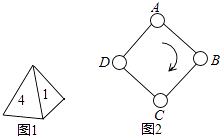
(1)嘉嘉随机掷一次骰子,求落回到圈A的概率P1;
(2)淇淇随机掷两次骰子,用列表法求最后落回到圈A的概率P2 , 并指出她与嘉嘉落回到圈A的可能性一样吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年疫情期间,某公司为了扩大经营,决定购进6台机器用于生产口罩.现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产口罩的数量如下表所示.经过预算,本次购买机器所耗资金不能超过36万元,
(1)按该公司要求可以有几种购买方案?
(2)如果该公司购进的6台机器的日生产能力不能低于42万个,那么为了节约资金应选择什么样的购买方案?
甲 | 乙 | |
价格(万元/台) | 7 | 5 |
每台日产量(万个) | 10 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①、图②,在给定的一张矩形纸片上作一个正方形,甲、乙两人的作法如下:
甲:以点A为圆心,AD长为半径画弧,交AB于点E,以点D为圆心,AD长为半径画弧,交CD于点F,连接EF,则四边形AEFD即为所求;
乙:作∠DAB的平分线,交CD于点M,同理作∠ADC的平分线,交AB于点N,连接MN,则四边形ADMN即为所求.


对于以上两种作法,可以做出的判定是( )
A.甲正确,乙错误B.甲、乙均正确
C.乙正确,甲错误D.甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O,A在数轴上表示的数分别是0,l,将线段OA分成1000等份,其分点由左向右依次为M1,M2…M999;将线段OM1分成1000等份,其分点由左向右依次为N1,N2…N999;将线段ON1分成1000等份,其分点由左向右依次为P1,P2…P999.则点P314所表示的数用科学记数法表示为_____.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用两种方法证明“四边形的外角和等于360°”.
如图,∠DAE、∠ABF、∠BCG、∠CDH是四边形ABCD的四个外角.
求证:∠DAE+∠ABF+∠BCG+∠CDH=360°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从热气球C处测得地面A,B两点的俯角分别是30°、45°,如果此时热气球C处的高度CD为100米,点A,D,B在同一直线上,则AB两点的距离是( )
A.200米
B.200 ![]() 米
米
C.220 ![]() 米
米
D.100( ![]() )米
)米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com