
����Ŀ����ͼ1��һö�ʵؾ��ȵ������������ӣ������ĸ��沢�ֱ��������1��2��3��4����ͼ2��������ABCD���㴦����һ��Ȧ����Ȧ��Ϸ�Ĺ���Ϊ����Ϸ��ÿ��һ�����ӣ������ŵ�һ���ϵ������Ǽ������������εı�˳ʱ�뷽�������������߳���
�磺����ȦA��������һ������3����˳ʱ��������3���߳����䵽ȦD�����ڶ�������2���ʹ�D��ʼ˳ʱ��������2���߳����䵽ȦB����
����Ϸ�ߴ�ȦA������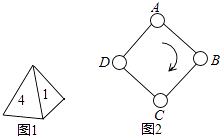
��1���μ������һ�����ӣ�����ص�ȦA�ĸ���P1��
��2����������������ӣ����б����������ص�ȦA�ĸ���P2 �� ��ָ������μ���ص�ȦA�Ŀ�����һ����
���𰸡�
��1���⣺�߹���4�ֵȿ��ܵĽ������ص�ȦA��ֻ��1�������
����ص�ȦA�ĸ���P1= ![]()
��2���⣺�б��ã�
1 | 2 | 3 | 4 | |
1 | ��1��1�� | ��2��1�� | ��3��1�� | ��4��1�� |
2 | ��1��2�� | ��2��2�� | ��3��2�� | ��4��2�� |
3 | ��1��3�� | ��2��3�� | ��3��3�� | ��4��3�� |
4 | ��1��4�� | ��2��4�� | ��3��4�� | ��4��4�� |
�߹���16�ֵȿ��ܵĽ���������ص�ȦA���У�1��3������2��2����3��1������4��4����
�������ص�ȦA�ĸ���P2= ![]() =
= ![]() ��
��
������μ���ص�ȦA�Ŀ�����һ��
����������1���μ������һ�����ӹ���4�ֵȿ��ܵĽ������ص�ȦA��ֻ��1����������ݸ��ʹ�ʽ������ʣ���2�����������г������ɱ���֪����16�ֵȿ��ܵĽ���������ص�ȦA����4�֣����ݸ��ʹ�ʽ��������ص�ȦA�ĸ��ʵó����ۡ�
�����㾫����������Ŀ����֪�����������б�������״ͼ�����ʹ�ʽ�����֪ʶ���Եõ�����Ĵ𰸣���Ҫ���յ�һ������Ҫ�����������������ʱ�����б����Ͳ������ˣ�Ϊ�˲��ز�©���г����п��ܵĽ����ͨ��������״ͼ������ʣ�һ��أ������һ�������У���n�ֿ��ܵĽ�����������Ƿ����Ŀ����Զ���ȣ��¼�A�������е�m�н������ô�¼�A�����ĸ���ΪP��A��=m/n��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У���E��F�ֱ��ڱ�AB��CD�ϣ��������������ж��ı���DEBFһ����ƽ���ı��ε��ǣ� ��

A.AE��CFB.DE��BFC.��ADE����CBFD.��AED����CFB
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=AC��AD����ABC�Ľ�ƽ���ߣ���OΪAB���е㣬����DO���ӳ�����E��ʹOE=OD������AE��BE��

��1����֤���ı���AEBD�Ǿ��Σ�
��2������ABC����ʲô����ʱ������AEBD�������Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ա�ADE����DAC��70������BAE��100����BC��DE�ཻ�ڵ�F�����DFB����Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1���Ķ����⣺

��ͼ�٣�����ABC�У���AB=8��AC=4����BC���ϵ�����AD��ȡֵ��Χ���� ��
��2������������ͼ�ڣ�����ABC��D��BC���ϵ��е㣬DE��DF�ڵ�D��DE��AB�ڵ�E��DF��AC�ڵ�F������EF����֤��BE+CF��EF��
��3��������չ����ͼ�ۣ����ı���ABCD�У���B+��D=180����CB=CD����BCD=140������CΪ������һ��70�ǵ����߷ֱ�AB��AD��E��F���㣬����EF��̽���߶�BE��DF��EF֮���������ϵ��������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��CD�����A����C����E����F�����������ϵ��(����)

A. ��A����C+��E+��F B. ��A+��E����C����F��180��
C. ��A����E+��C+��F��90�� D. ��A+��E+��C+��F��360��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b��ͼ���뷴��������y=![]() ��ͼ���ڵ�A����3��m+8����B��n����6�����㣮
��ͼ���ڵ�A����3��m+8����B��n����6�����㣮
��1����һ�κ����뷴���������Ľ���ʽ��
��2������AOB�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ƽ��ֱ������ϵ�У�A(a��3)��B(b��6)��C(c��1)��a��b��c��Ϊʵ������������3b��5c����2a��18��4b��c��3a��10
(1) ��ֱ���ú�a�Ĵ���ʽ��ʾb��c
(2) ��ʵ��a�仯ʱ���ж���ABC������Ƿ����仯�������䣬����ֵ�����仯������仯��Χ
(3) ��ʵ��a�仯ʱ�����߶�AB��y���ཻ���߶�OB���߶�AC���ڵ�P����S��PAB��S��PBC����ʵ��a��ȡֵ��Χ.


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
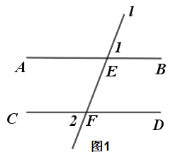
����Ŀ����֪��ֱ��l�ֱ�AB��CD��E��F���㣬��AB��CD��
��1�� ˵������1=��2��
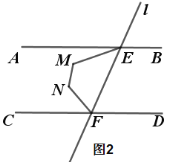
��2�� ��ͼ2����M��N��AB��CD֮�䣬����ֱ��l��࣬����EMN+��FNM=260����
������AEM+��CFN�Ķ�����
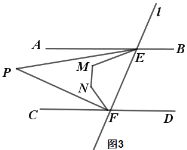
����ͼ3����EPƽ����AEM��FPƽ����CFN������P�Ķ�����
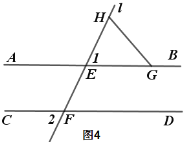
��3�� ��ͼ4����2=80������G������EB�ϣ���H��AB�Ϸ���ֱ��l�ϣ���Q��ƽ����һ�㣬����QG��QH������AGQ=18������FHQ=24����ֱ��д����GQH�Ķ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com