
【题目】(1)阅读理解:

如图①,在△ABC中,若AB=8,AC=4,求BC边上的中线AD的取值范围是
(2)问题解决:如图②,在△ABC中D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以C为顶点作一个70角的两边分别交AB,AD于E,F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.
【答案】(1)2<AD<6;(2)证明见解析;(3)BE+DF=EF,证明见解析
【解析】
(1)如图1(见解析),先根据三角形全等的判定定理与性质得出![]() ,再根据三角形的三边关系定理即可得;
,再根据三角形的三边关系定理即可得;
(2)如图2(见解析),先同(1),根据三角形全等的判定定理与性质得出![]() ,再根据垂直平分线的判定与性质得出
,再根据垂直平分线的判定与性质得出![]() ,然后根据三角形的三边关系定理、等量代换即可得证;
,然后根据三角形的三边关系定理、等量代换即可得证;
(3)如图3(见解析),先根据角的和差得出![]() ,再根据三角形全等的判定定理与性质可得
,再根据三角形全等的判定定理与性质可得![]() ,
,![]() ,从而可得
,从而可得![]() ,然后根据三角形全等的判定定理与性质可得
,然后根据三角形全等的判定定理与性质可得![]() ,最后根据线段的和差、等量代换即可得.
,最后根据线段的和差、等量代换即可得.
(1)如图1,延长AD至E,使![]() ,连接BE
,连接BE
∵AD是BC边上的中线
∴![]()
在![]() 和
和![]() 中,
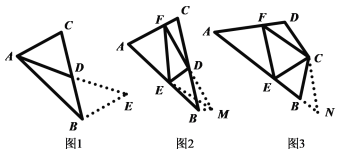
中,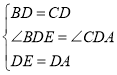
∴![]()
∴![]()
在![]() 中,由三角形的三边关系得:
中,由三角形的三边关系得:![]()
∴![]() ,即
,即![]()
∴![]() ,即
,即![]()
∴![]()
故答案为:![]() ;
;
(2)如图2,延长FD至点M,使![]() ,连接BM、EM
,连接BM、EM
同(1)得:![]()
∴![]()
∵![]() ,
,![]()
∴![]() 是
是![]() 的垂直平分线
的垂直平分线
∴![]()
在![]() 中,由三角形的三边关系得:
中,由三角形的三边关系得:![]()
∴![]() ;
;
(3)![]() ;证明如下:
;证明如下:
如图3,延长AB至点N,使![]() ,连接CN
,连接CN
∵![]() ,
,![]()
∴![]()
在![]() 和
和![]() 中,
中,
∴![]()
∴![]() ,
,![]()
∵![]() ,
,![]()
∴![]()
∴![]()
∴![]()
在![]() 和
和![]() 中,
中,
∴![]()
∴![]()
∵![]()
∴![]() .
.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】在直角坐标系中,△ABO的顶点坐标分别为O(0,0)、A(2a,0)、B(0,﹣a),线段EF两端点坐标为E(﹣m,a+1),F(﹣m,1)(2a>m>a);直线l∥y轴交x轴于P(a,0),且线段EF与CD关于y轴对称,线段CD与NM关于直线l对称.
(1)求点N、M的坐标(用含m、a的代数式表示);
(2)△ABO与△MFE通过平移能重合吗?能与不能都要说明其理由,若能请你说出一个平移方案(平移的单位数用m、a表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了抓住梵净山文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是一棵大树,BF是一个斜坡,坡角为30°,某时刻太阳光直射斜坡BF,树顶端A的影子落到斜坡上的点D处,已知BC=6m,BD=4m,求树高AC的高度(结果精确到0.1m,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.

(1)如图1,直接写出∠A和∠C之间的数量关系___;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E. F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字1,2,3,4.如图2,正方形ABCD顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.
如:若从圈A起跳,第一次掷得3,就顺时针连续跳3个边长,落到圈D;若第二次掷得2,就从D开始顺时针连续跳2个边长,落到圈B;…
设游戏者从圈A起跳.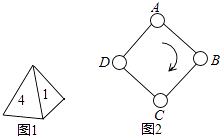
(1)嘉嘉随机掷一次骰子,求落回到圈A的概率P1;
(2)淇淇随机掷两次骰子,用列表法求最后落回到圈A的概率P2 , 并指出她与嘉嘉落回到圈A的可能性一样吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠C=90°,BC=8厘米,点D在AC上,CD=3厘米.点P、Q分别由A,C两点同时出发,点P沿AC方向向点C匀速移动,速度为每秒k厘米,行完AC全程用时8秒;点Q沿CB方向向点B匀速移动,速度为每秒1厘米.设运动的时间为x秒(0<x<8),△DCQ的面积为y1平方厘米,△PCQ的面积为y2平方厘米.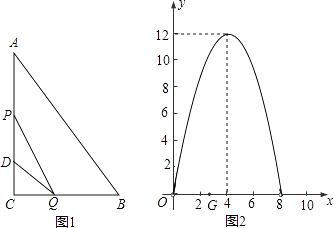
(1)求y1与x的函数关系,并在图2中画出y1的图象;
(2)如图2,y2的图象是抛物线的一部分,其顶点坐标是(4,12),求点P的速度及AC的长;
(3)在图2中,点G是x轴正半轴上一点0<OG<6,过G作EF垂直于x轴,分别交y1、y2的图象于点E、F.
①说出线段EF的长在图1中所表示的实际意义;
②当0<x<6时,求线段EF长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校德育处组织“四品八德”好少年评比活动,每班只有一个名额.现某班有甲、乙、丙三名学生参与竞选,第一轮根据“品行规范”、“学习规范”进行量化考核.甲乙丙他们的量化考核成绩(单位:分)分别用两种方式进行了统计,如下表和图1:


(1)请将表和图1中的空缺部分补充完整;
(2)竞选的第二轮是由本班的50位学生进行投票,每票计6分,甲、乙、丙三人的得票情况如图2(没有弃权票,每名学生只能选一人).
①若将“品行规范”、“学习规范”、“得票”三项测试得分按4:3:3的比例确定最后成绩,通过计算谁将会被推选为校“四品八德”好少年.
②若规定得票测试分占20%,要使甲学生最后得分不低于91分,则“品行规范”成绩在总分中所占比例的取值范围应是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com