
【题目】在直角坐标系中,△ABO的顶点坐标分别为O(0,0)、A(2a,0)、B(0,﹣a),线段EF两端点坐标为E(﹣m,a+1),F(﹣m,1)(2a>m>a);直线l∥y轴交x轴于P(a,0),且线段EF与CD关于y轴对称,线段CD与NM关于直线l对称.
(1)求点N、M的坐标(用含m、a的代数式表示);
(2)△ABO与△MFE通过平移能重合吗?能与不能都要说明其理由,若能请你说出一个平移方案(平移的单位数用m、a表示)

【答案】(1)M(2a﹣m,a+1),N(2a﹣m,1);(2)能重合
【解析】
(1)先根据EF与CD关于y轴对称,得到C,D两端点坐标,再设CD与直线l之间的距离为x,根据CD与MN关于直线l对称,l与y轴之间的距离为a,求得M的横坐标即可;(2)先判定△ABO≌△MFE,得出△ABO与△MFE通过平移能重合,再根据对应点的位置,写出平移方案即可.
(1)∵EF与CD关于y轴对称,EF两端点坐标为E(﹣m,a+1),F(﹣m,1),
∴C(m,a+1),D(m,1),
设CD与直线l之间的距离为x,
∵CD与MN关于直线l对称,l与y轴之间的距离为a,
∴MN与y轴之间的距离为a﹣x,
∵x=m﹣a,
∴M的横坐标为a﹣(m﹣a)=2a﹣m,
∴M(2a﹣m,a+1),N(2a﹣m,1);
(2)能重合.
∵EM=2a﹣m﹣(﹣m)=2a=OA,EF=a+1﹣1=a=OB,
又∵EF∥y轴,EM∥x轴,
∴∠MEF=∠AOB=90°,
∴△ABO≌△MFE(SAS),
∴△ABO与△MFE通过平移能重合.
平移方案:将△ABO向上平移(a+1)个单位后,再向左平移m个单位,即可重合.


科目:初中数学 来源: 题型:
【题目】如图所示,在下列条件中,不能作为判断△ABD≌△BAC的条件是( )

A. ∠D=∠C,∠BAD=∠ABC B. ∠BAD=∠ABC,∠ABD=∠BAC
C. BD=AC,∠BAD=∠ABC D. AD=BC,BD=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
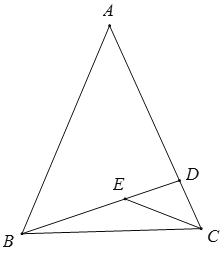
【题目】如图,在△ABC中,BD⊥AC于D.若∠A:∠ABC:∠ACB=3:4:5,E为线段BD上任一点.
(1)试求∠ABD的度数;
(2)求证:∠BEC>∠A.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“双十二”期间,A,B两个超市开展促销活动,活动方式如下:
A超市:购物金额打9折后,若超过2000元再优惠300元;
B超市:购物金额打8折.
某学校计划购买某品牌的篮球做奖品,该品牌的篮球在A,B两个超市的标价相同.根据商场的活动方式:
(1)若一次性付款4200元购买这种篮球,则在B商场购买的数量比在A商场购买的数量多5个.请求出这种篮球的标价;
(2)学校计划购买100个篮球,请你设计一个购买方案,使所需的费用最少.(直接写出方案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雷达二维平面定位的主要原理是:测量目标的两个信息―距离和角度,目标的表示方法为![]() ,其中,m表示目标与探测器的距离;
,其中,m表示目标与探测器的距离;![]() 表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为
表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为![]() ,目标C的位置表示为
,目标C的位置表示为![]() .用这种方法表示目标B的位置,正确的是( )
.用这种方法表示目标B的位置,正确的是( )

A. (-4, 150°) B. (4, 150°) C. (-2, 150°) D. (2, 150°)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx﹣2(k>0)与双曲线 ![]() 在第一象限内的交点R,与x轴、y轴的交点分别为P、Q.过R作RM⊥x轴,M为垂足,若△OPQ与△PRM的面积相等,则k的值等于 .
在第一象限内的交点R,与x轴、y轴的交点分别为P、Q.过R作RM⊥x轴,M为垂足,若△OPQ与△PRM的面积相等,则k的值等于 . 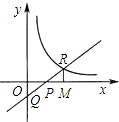
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx﹣2(k>0)与双曲线 ![]() 在第一象限内的交点R,与x轴、y轴的交点分别为P、Q.过R作RM⊥x轴,M为垂足,若△OPQ与△PRM的面积相等,则k的值等于 .
在第一象限内的交点R,与x轴、y轴的交点分别为P、Q.过R作RM⊥x轴,M为垂足,若△OPQ与△PRM的面积相等,则k的值等于 . 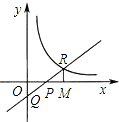
查看答案和解析>>
科目:初中数学 来源: 题型:
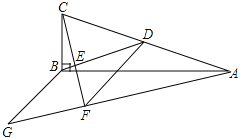
【题目】在![]() 中,
中,![]() ,BD为AC边上的中线,过点C作
,BD为AC边上的中线,过点C作![]() 于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取
于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取![]() ,连接BG,DF.
,连接BG,DF.
![]() 求证:
求证:![]() ;
;
![]() 求证:四边形BDFG为菱形;
求证:四边形BDFG为菱形;
![]() 若
若![]() ,
,![]() ,求四边形BDFG的周长.
,求四边形BDFG的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京东商城销售A、B两种型号的电风扇,销售单价分别为250元、180元,如表是近两周的销售利润情况:(进价、售价均保持不变,利润=销售收入﹣进货成本)

(1)求A、B两种型号电风扇的每台进价;
(2)若京东商城准备用不多于5万元的金额采购这两种型号的电风扇共300台,求A种型号的电风扇最多能采购多少台?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com