
【题目】如图,AC是一棵大树,BF是一个斜坡,坡角为30°,某时刻太阳光直射斜坡BF,树顶端A的影子落到斜坡上的点D处,已知BC=6m,BD=4m,求树高AC的高度(结果精确到0.1m,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
【答案】解:如图,过点D作DP⊥BE于点P,作DQ⊥AC于点Q,

∵∠DBP=30°、BD=4,
∴CQ=DP= ![]() BD=2,BP=BDcos∠DBP=4×
BD=2,BP=BDcos∠DBP=4× ![]() =2
=2 ![]() ,
,
则DQ=CP=BP+BC=2 ![]() +6,
+6,
∵太阳光直射斜坡BF,
∴∠ADB=90°
又∵∠QDB=∠DBP=30°,
∴∠ADQ=60°,
则AQ=DQtan∠ADQ=(2 ![]() +6)
+6) ![]() =6+6
=6+6 ![]() ,
,
∴树高AC=AQ+CQ=6+6 ![]() +2=8+6
+2=8+6 ![]() ≈18.4(m),
≈18.4(m),
答:树高AC的高度约为18.4m.
【解析】过点D作DP⊥BE于点P,作DQ⊥AC于点Q,∠DBP=30°、BD=4,CQ=DP= ![]() BD=2,BP=BDcos∠DBP,则DQ=CP=BP+BC,在Rt△ADQ中由解三角函数得出AQ=DQtan∠ADQ进而找到树高。
BD=2,BP=BDcos∠DBP,则DQ=CP=BP+BC,在Rt△ADQ中由解三角函数得出AQ=DQtan∠ADQ进而找到树高。


科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,以AD为弦的⊙O交AB,AC于E,F,已知EF∥BC.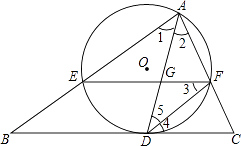
(1)求证:BC是⊙O的切线;
(2)若已知AE=9,CF=4,求DE长;
(3)在(2)的条件下,若∠BAC=60°,求tan∠AFE的值及GD长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=a,DH=4,平移距离CF为a-2,试用a的代数式表示阴影部分的面积____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.

(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中, AD为∠BAC的平分线,AF为BC边上的高.
(1)若∠B=38°,∠C=76°,求∠DAF的度数.
(2)若∠B=m°,∠C=n°,(m<n).求∠DAF的度数(用含m、n的式子表示).
(3)若∠C-∠B=30°,则∠DAF=_________度.(填空)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读理解:

如图①,在△ABC中,若AB=8,AC=4,求BC边上的中线AD的取值范围是
(2)问题解决:如图②,在△ABC中D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以C为顶点作一个70角的两边分别交AB,AD于E,F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在数轴上点A,点B对应的数分别是6,﹣6,∠DCE=90°(点C与点O重合,点D在数轴的正半轴上)
(1)如图1,若CF平分∠ACE,则∠AOF= 度;点A与点B的距离=
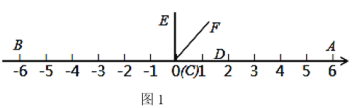
(2)如图2,将∠DCE沿数轴的正半轴向右平移t(0<t<3)个单位后,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α.

①当t=1时,α= ;点B与点C的距离=
②猜想∠BCE和α的数量关系,并说明理由;
(3)如图3,开始∠D1C1E1与∠DCE重合,将∠DCE沿数轴的正半轴向右平移t(0![]() t
t![]() 3)个单位,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α,与此同时,将∠D1C1E1沿数轴的负半轴向左平移t(0
3)个单位,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α,与此同时,将∠D1C1E1沿数轴的负半轴向左平移t(0![]() t
t![]() 3)个单位,再绕点顶点C1顺时针旋转30t度,作C1F1平分∠AC1E1,记∠D1C1F1=β,若α与β满足|α﹣β|=20°,求t的值.
3)个单位,再绕点顶点C1顺时针旋转30t度,作C1F1平分∠AC1E1,记∠D1C1F1=β,若α与β满足|α﹣β|=20°,求t的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com