
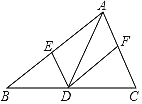
【题目】如图,AD是△ABC的角平分线,以AD为弦的⊙O交AB,AC于E,F,已知EF∥BC.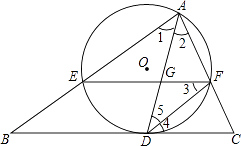
(1)求证:BC是⊙O的切线;
(2)若已知AE=9,CF=4,求DE长;
(3)在(2)的条件下,若∠BAC=60°,求tan∠AFE的值及GD长.
【答案】
(1)证明:连接OD, 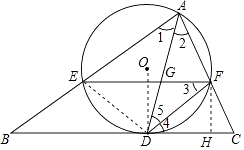
∵AD是△ABC的角平分线,
∴∠1=∠2,
∴ ![]() =
= ![]() ,
,
∴OD⊥EF,
∵EF∥BC,
∴OD⊥BC,
∴BC是⊙O的切线
(2)解:连接DE,
∵ ![]() =
= ![]() ,
,
∴DE=DF,
∵EF∥BC,
∴∠3=∠4,
∵∠1=∠3,
∴∠1=∠4,
∵∠DFC=∠AED,
∴△AED∽△DFC,
∴ ![]() ,即
,即 ![]() ,
,
∴DE2=36,
∴DE=6
(3)解:过F作FH⊥BC于H,
∵∠BAC=60°,
∴∠1=∠2=∠3=∠4=30°,
∴FH= ![]() DF=
DF= ![]() =3,DH=3
=3,DH=3 ![]() ,
,
∴CH= ![]() =
= ![]() ,
,
∵EF∥BC,
∴∠C=∠AFE,
∴tan∠AFE=tan∠C= ![]() =
= ![]() ;
;
∵∠4=∠2.∠C=∠C,
∴△ADC∽△DFC,
∴ ![]() ,
,
∵∠5=∠5,∠3=∠2,
∴△ADF∽△FDG,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴DG= ![]() .
.
【解析】(1)连半径,证垂直。连接OD,由AD是△ABC的角平分线。得出圆周角相等,继而得弧相等,根据垂径定理得出OD⊥EF,再根据EF∥BC,得到OD⊥BC,即可得证。
(2)先证明DE=DF,再证明△AED∽△DFC,根据相似三角形的性质得对应边成比例,即可求出DE的长。
(3)抓住已知∠BAC=60°,既可以证得∠4=30°,由此添加辅助线过F作FH⊥BC于H,Rt△DFH和Rt△FHC中就可以求出线段FH、DH、CH的长,根据平行得角相等,即可求出an∠AFE的值,再证明△ADC∽△DFC和△ADF∽△FDG,找到中间比,继而就可以求出DG的长。
【考点精析】解答此题的关键在于理解垂径定理的相关知识,掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,以及对切线的判定定理的理解,了解切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.


科目:初中数学 来源: 题型:
【题目】计算题
1、计算、![]() +(
+(![]() )﹣1﹣4tan45° 2、 解方程:x2=3x.
)﹣1﹣4tan45° 2、 解方程:x2=3x.
(1)计算: ![]() +(
+( ![]() )﹣1﹣4tan45°
)﹣1﹣4tan45°
(2)解方程:x2=3x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B,C在反比例函数y= ![]() (x>0)的图象上,若△OAB的面积等于6,则k的值为( )
(x>0)的图象上,若△OAB的面积等于6,则k的值为( )
A.2
B.4
C.6
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD折叠,使点C与A点重合,折痕为EF.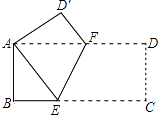
(1)判断四边形AFCE的形状,并说明理由.
(2)若AB=4,BC=8,求折痕EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温度的变化是人们经常谈论的话题,请根据图象与同伴讨论某天温度变化的情况.
(1)这一天的最高温度是多少?是在几时到达的?最低温度呢?
(2)这一天的温差是多少?从最低温度到最高温度经过多长时间?
(3)在什么时间范围内温度在上升?在什么时间范围内温度在下降?
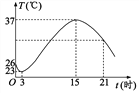
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,△ABO的顶点坐标分别为O(0,0)、A(2a,0)、B(0,﹣a),线段EF两端点坐标为E(﹣m,a+1),F(﹣m,1)(2a>m>a);直线l∥y轴交x轴于P(a,0),且线段EF与CD关于y轴对称,线段CD与NM关于直线l对称.
(1)求点N、M的坐标(用含m、a的代数式表示);
(2)△ABO与△MFE通过平移能重合吗?能与不能都要说明其理由,若能请你说出一个平移方案(平移的单位数用m、a表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,点 D 是边 BC 上的点(与 B、C 两点不重合),过点 D作 DE∥AC,DF∥AB,分别交 AB、AC 于 E、F 两点,下列说法正确的是( )
A. 若 AD 平分∠BAC,则四边形 AEDF 是菱形
B. 若 BD=CD,则四边形 AEDF 是菱形
C. 若 AD 垂直平分 BC,则四边形 AEDF 是矩形
D. 若 AD⊥BC,则四边形 AEDF 是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是一棵大树,BF是一个斜坡,坡角为30°,某时刻太阳光直射斜坡BF,树顶端A的影子落到斜坡上的点D处,已知BC=6m,BD=4m,求树高AC的高度(结果精确到0.1m,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com