
【题目】如图,将矩形ABCD折叠,使点C与A点重合,折痕为EF.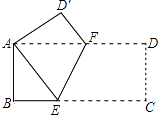
(1)判断四边形AFCE的形状,并说明理由.
(2)若AB=4,BC=8,求折痕EF的长.
【答案】
(1)解:四边形AFCE是菱形,
理由:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠EAO=∠FCO,
由折叠的性质可得:OA=OC,AE=CE,AF=CF,
在△OAE和△OCF中,
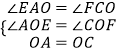 ,
,
∴△AEO≌△CFO(AAS),
∴AE=CF,
∴AE=CE=CF=AF,
∴四边形AFCE是菱形
(2)解:连接AC交EF于点O,
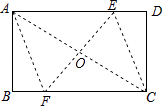
由勾股定理知AC=4 ![]() ,
,
又∵折叠矩形使C与A重合时有EF⊥AC,
则Rt△EOC∽Rt△ABC,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴OE= ![]() OC=
OC= ![]() ×2
×2 ![]() ,
,
故EF=2OE=2 ![]() .
.
【解析】(1)抓住已知条件,将矩形ABCD折叠,使点C与A点重合,根据矩形的性质和折叠的性质得出OA=OC,AE=CE,AF=CF,∠EAO=∠FCO,,再证明△AEO≌△CFO,从而得出AE=CF,即可证明四边形AFCE的四边相等,即可得出结论。
(2)根据勾股定理求出AC的长,再证明Rt△EOC∽Rt△ABC,根据相似三角形的对应边成比例,建立方程,求出OE的长,即可得到EF的长。
【考点精析】解答此题的关键在于理解菱形的判定方法的相关知识,掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形,以及对矩形的性质的理解,了解矩形的四个角都是直角,矩形的对角线相等.


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两人分别从![]() ,
,![]() 两地相向而行,他们距
两地相向而行,他们距![]() 地的距离
地的距离![]() 与时间
与时间![]() 的关系如图所示,下列说法错误的是( )
的关系如图所示,下列说法错误的是( )

A.甲的速度是![]() B.甲出发4.5小时后与乙相遇
B.甲出发4.5小时后与乙相遇
C.乙比甲晚出发2小时D.乙的速度是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 的方格中,每一个小方格的边长为1,点
的方格中,每一个小方格的边长为1,点![]() 在小方格的顶点上,请按下列要求分别画出一个以点
在小方格的顶点上,请按下列要求分别画出一个以点![]() 为顶点的四边形,且所画四边形的四个顶点都在小方格的顶点上.
为顶点的四边形,且所画四边形的四个顶点都在小方格的顶点上.

(1)在图①中画一个一般的平行四边形(非矩形或菱形),面积为6.
(2)在图②中画一个菱形或正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,求∠HPQ的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现在要生产甲乙两种产品,甲产品需要A原料15千克,B原料20千克 ;乙产品需要A原料20千克,B原料10千克.现在A原料有360千克,B原料300千克.现在要生产甲乙两种产品共20件.
(1)共有几种方案
(2)已知生产甲产品成本是每件10元,乙产品成本每件8元.那么生产多少件甲产品可以使生产成本最低?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,以AD为弦的⊙O交AB,AC于E,F,已知EF∥BC.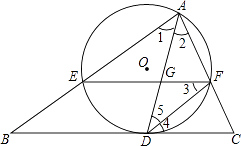
(1)求证:BC是⊙O的切线;
(2)若已知AE=9,CF=4,求DE长;
(3)在(2)的条件下,若∠BAC=60°,求tan∠AFE的值及GD长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+b2﹣4ac与反比例函数y= ![]() 在同一坐标系内的图象大致为( )
在同一坐标系内的图象大致为( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,抛物线 ![]() 过点A(6,0)和点B(3,
过点A(6,0)和点B(3, ![]() ).
).
(1)求抛物线y1的解析式;
(2)将抛物线y1沿x轴翻折得抛物线y2 , 求抛物线y2的解析式;
(3)在(2)的条件下,抛物线y2上是否存在点M,使△OAM与△AOB相似?如果存在,求出点M的坐标;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中, AD为∠BAC的平分线,AF为BC边上的高.
(1)若∠B=38°,∠C=76°,求∠DAF的度数.
(2)若∠B=m°,∠C=n°,(m<n).求∠DAF的度数(用含m、n的式子表示).
(3)若∠C-∠B=30°,则∠DAF=_________度.(填空)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com