
【题目】现在要生产甲乙两种产品,甲产品需要A原料15千克,B原料20千克 ;乙产品需要A原料20千克,B原料10千克.现在A原料有360千克,B原料300千克.现在要生产甲乙两种产品共20件.
(1)共有几种方案
(2)已知生产甲产品成本是每件10元,乙产品成本每件8元.那么生产多少件甲产品可以使生产成本最低?
【答案】(1)3种方案;(2)176元.
【解析】
(1)设生产甲产品x件,根据A、B原料的消耗列出关于x的一元一次不等式组,解不等式得出x的取值范围,即可得到答案;
(2)令生产成本为y,找出生产成本y关于生产甲产品x件的函数关系式,由一次函数的性质和x的取值范围即可得出结论.
解:(1)设生产甲产品x件,则生产乙产品(20-x)件,
![]() ,
,
解得:![]() ,
,
∵x取正整数,
则x=8,x=9,x=10,
∴生产甲产品8件,乙产品12件;
生产甲产品9件,乙产品11件;
生产甲产品10件,乙产品10件;
∴共有3种方案;
(2)设生产成本为y元,由题意可知:
y=10x+8(20-x)=2x+160,
∵y随x的增大而增大,
∴当x=8时,y最小,最小值为:2×8+160=176元.
答:生产8件甲产品可以使生产成本最低,最低成本为176元.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点A,C,D在⊙O上,过D作PF∥AC交⊙O于F,交AB于E,且∠BPF=∠ADC.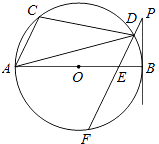
(1)判断直线BP和⊙O的位置关系,并说明你的理由;
(2)当⊙O的半径为 ![]() ,AC=2,BE=1时,求BP的长.
,AC=2,BE=1时,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店取厂家选购甲、乙两种商品,乙商品每件进价比甲商品每件进价多20元,若购进甲商品5件和乙商品4件共需要800元;
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)若甲种商品的售价为每件100元,乙种商品的售价为每件125元,该商店准备购进甲、乙两种商品共40件,且这两种商品全部售出后总利润不少于900元,则甲种商品最多可购进多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校决定在4月7日开展“世界无烟日”宣传活动,活动有A社区板报、B集会演讲、C喇叭广播、D发宣传画四种宣传方式.学校围绕“你最喜欢的宣传方式是什么?”在全校学生中进行随机抽样调查(四个选项中必选且只选一项),根据调查统计结果,绘制了两种不完整的统计图表:
选项 | 方式 | 百分比 |
A | 社区板报 | 35% |
B | 集会演讲 | m |
C | 喇叭广播 | 25% |
D | 发宣传画 | 10% |
请结合统计图表,回答下列问题:
(1)本次抽查的学生共人,m= , 并将条形统计图补充完整;
(2)若该校学生有1500人,请你估计该校喜欢“集会演讲”这项宣传方式的学生约有多少人?
(3)学校采用抽签方式让每班在A、B、C、D四种宣传方式在随机抽取两种进行展示,请用树状图或列表法求某班所抽到的两种方式恰好是“集会演讲”和“喇叭广播”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(0,0),B(0,4),C(3,t+4),D(3,t). 记N(t)为![]() ABCD内部(不含边界)整点的个数,其中整点是指横坐标和纵坐标都是整数的点,则N(t)所有可能的值为
ABCD内部(不含边界)整点的个数,其中整点是指横坐标和纵坐标都是整数的点,则N(t)所有可能的值为
A. 6、7B. 7、8C. 6、7、8D. 6、8、9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD折叠,使点C与A点重合,折痕为EF.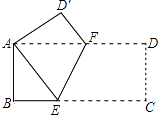
(1)判断四边形AFCE的形状,并说明理由.
(2)若AB=4,BC=8,求折痕EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按照有关规定,距高铁轨道![]() 米以内的区域内不宜临路新建学校、医院、敬老院和集中住宅区等噪声敏感建筑物.如图是一个小区平面示意图,长方形
米以内的区域内不宜临路新建学校、医院、敬老院和集中住宅区等噪声敏感建筑物.如图是一个小区平面示意图,长方形![]() 为一新建小区,直线
为一新建小区,直线![]() 为高铁轨道,
为高铁轨道,![]() 是直线
是直线![]() 上的两点,点
上的两点,点![]() 在一条直线上,且
在一条直线上,且![]() .小王看中了
.小王看中了![]() 号楼
号楼![]() 单元的一套住宅,与售楼人员的对话如下:
单元的一套住宅,与售楼人员的对话如下:
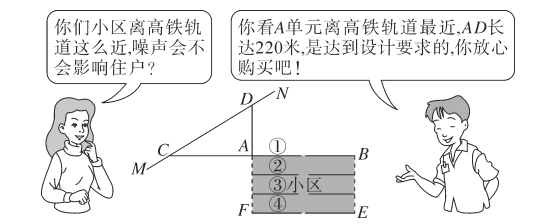
![]() 小王心中一算,发现售楼人员的话不可信,请你用所学的数学知识说明理由;
小王心中一算,发现售楼人员的话不可信,请你用所学的数学知识说明理由;
![]() 若一列长度为
若一列长度为![]() 米的高铁以
米的高铁以![]() 千米/时的速度通过,则
千米/时的速度通过,则![]() 单元用户受到影响的时间有多长?
单元用户受到影响的时间有多长?
(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O,A两处观测P处,仰角分别为α、β,且tanα= ![]() ,tan
,tan ![]() ,以O为原点,OA所在直线为x轴建立直角坐标系.
,以O为原点,OA所在直线为x轴建立直角坐标系.
(1)求点P的坐标;
(2)水面上升1m,水面宽多少( ![]() 取1.41,结果精确到0.1m)?
取1.41,结果精确到0.1m)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )

A. 3 B. 4 C. 6 D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com