Question

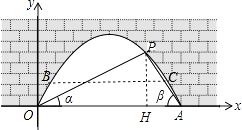
【题目】图中是抛物线拱桥，P处有一照明灯，水面OA宽4m，从O，A两处观测P处，仰角分别为α、β，且tanα= ，tan ，以O为原点，OA所在直线为x轴建立直角坐标系．

（1）求点P的坐标；
（2）水面上升1m，水面宽多少（ 取1.41，结果精确到0.1m）？

Answer 1

【答案】
（1）解：过点P作PH⊥OA于H，如图．

；

设PH=3x，

在Rt△OHP中，

∵tanα= = ，

∴OH=6x．

在Rt△AHP中，

∵tanβ= = ，

∴AH=2x，

∴OA=OH+AH=8x=4，

∴x= ，

∴OH=3，PH= ，

∴点P的坐标为（3， ）

（2）解：若水面上升1m后到达BC位置，如图，

过点O（0，0），A（4，0）的抛物线的解析式可设为y=ax（x﹣4），

∵P（3， ）在抛物线y=ax（x﹣4）上，

∴3a（3﹣4）= ，

解得a=﹣ ，

∴抛物线的解析式为y=﹣ x（x﹣4）．

当y=1时，﹣ x（x﹣4）=1，

解得x1=2+ ，x2=2﹣ ，

∴BC=（2+ ）﹣（2﹣ ）=2 =2×1.41=2.82≈2.8．

答：水面上升1m，水面宽约为2.8米

【解析】（1）过点P作PH⊥OA于H，设PH=3x，在Rt△OHP中，由tanα得出OH=6x，在在Rt△AHP中，由tanβ得出AH=2x，然后由OA=OH+AH=8x=4，求出X的值，进而知OH、PH的长度，找到P点的坐标；（2）若水面上升1m后到达BC位置，由待定系数法求出抛物线的解析式，然后把Y=1代入解析式求出X的值进而找到BC的长度。
【考点精析】通过灵活运用关于仰角俯角问题，掌握仰角：视线在水平线上方的角；俯角：视线在水平线下方的角即可以解答此题．