
【题目】下面的图表是我国数学家发明的“杨辉三角”,此图揭示了![]() (n为非负整数)的展开式的项数及各项系数的有关规律.请你观察,并根据此规律写出:
(n为非负整数)的展开式的项数及各项系数的有关规律.请你观察,并根据此规律写出:![]() _________.
_________.

【答案】a5-5a4b+10a3b2-10a2b3+5ab4-b5
【解析】
仿照![]() 的展开式的项数及各项系数的有关规律将
的展开式的项数及各项系数的有关规律将![]() 展开,即可得出
展开,即可得出![]() 的展开式.
的展开式.
解:由(1)“杨辉三角”可知:![]() 的第一项系数为1,第二项系数由上一层的相邻两数之和求得,……以此类推,
的第一项系数为1,第二项系数由上一层的相邻两数之和求得,……以此类推,
故![]() 展开式的各项系数如下图所示
展开式的各项系数如下图所示

根据右侧展开式可知:![]() 的展开式第一项a的指数为n,b的指数为0,第二项a的指数为n-1,b的指数为1,第三项a的指数为n-2,b的指数为2,……以此类推
的展开式第一项a的指数为n,b的指数为0,第二项a的指数为n-1,b的指数为1,第三项a的指数为n-2,b的指数为2,……以此类推
∴![]() = a5+5a4b+10a3b2+10a2b3+5ab4+b5
= a5+5a4b+10a3b2+10a2b3+5ab4+b5
∴![]() =
=![]() = a5+5a4(-b)+10a3(-b)2+10a2(-b)3+5a(-b)4+(-b)5
= a5+5a4(-b)+10a3(-b)2+10a2(-b)3+5a(-b)4+(-b)5
= a5-5a4b+10a3b2-10a2b3+5ab4-b5
故答案为:a5-5a4b+10a3b2-10a2b3+5ab4-b5.


科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,M是边BC延长线上一点,连接AM交△ABC的外接圆于点D,延长BD至N,使得BN=AM,连接CN、MN,
(1)求证:△CMN是等边三角形;
(2)判断CN与⊙O的位置关系,并说明理由;
(3)若AD:AB=3:4,BN=4,求等边△ABC的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点A,C,D在⊙O上,过D作PF∥AC交⊙O于F,交AB于E,且∠BPF=∠ADC.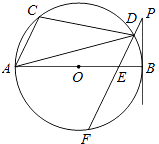
(1)判断直线BP和⊙O的位置关系,并说明你的理由;
(2)当⊙O的半径为 ![]() ,AC=2,BE=1时,求BP的长.
,AC=2,BE=1时,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,AB=CD,点E,F在BC上,且BE=CF.
(1)求证:△ABE≌△DCF;
(2)试证明:以A,F,D,E为顶点的四边形是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示正整数后,背面朝上,洗匀放好,现从中随机抽取一张,不放回,再从剩下的卡片中随机抽取一张.
(1)请用树状图或列表的方法表示两次抽取卡片的所有可能出现的结果,(卡片用A,B,C,D表示);
(2)我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,求抽到的两张卡片上的数都是勾股数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=150°,AC=4,tanB= ![]() .
.
(1)求BC的长;
(2)利用此图形求tan15°的值(精确到0.1,参考数据: ![]() =1.4,
=1.4, ![]() =1.7,
=1.7, ![]() =2.2)
=2.2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店取厂家选购甲、乙两种商品,乙商品每件进价比甲商品每件进价多20元,若购进甲商品5件和乙商品4件共需要800元;
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)若甲种商品的售价为每件100元,乙种商品的售价为每件125元,该商店准备购进甲、乙两种商品共40件,且这两种商品全部售出后总利润不少于900元,则甲种商品最多可购进多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校决定在4月7日开展“世界无烟日”宣传活动,活动有A社区板报、B集会演讲、C喇叭广播、D发宣传画四种宣传方式.学校围绕“你最喜欢的宣传方式是什么?”在全校学生中进行随机抽样调查(四个选项中必选且只选一项),根据调查统计结果,绘制了两种不完整的统计图表:
选项 | 方式 | 百分比 |
A | 社区板报 | 35% |
B | 集会演讲 | m |
C | 喇叭广播 | 25% |
D | 发宣传画 | 10% |
请结合统计图表,回答下列问题:
(1)本次抽查的学生共人,m= , 并将条形统计图补充完整;
(2)若该校学生有1500人,请你估计该校喜欢“集会演讲”这项宣传方式的学生约有多少人?
(3)学校采用抽签方式让每班在A、B、C、D四种宣传方式在随机抽取两种进行展示,请用树状图或列表法求某班所抽到的两种方式恰好是“集会演讲”和“喇叭广播”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O,A两处观测P处,仰角分别为α、β,且tanα= ![]() ,tan
,tan ![]() ,以O为原点,OA所在直线为x轴建立直角坐标系.
,以O为原点,OA所在直线为x轴建立直角坐标系.
(1)求点P的坐标;
(2)水面上升1m,水面宽多少( ![]() 取1.41,结果精确到0.1m)?
取1.41,结果精确到0.1m)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com