
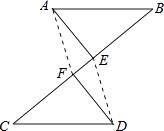
【题目】如图,AB∥CD,AB=CD,点E,F在BC上,且BE=CF.
(1)求证:△ABE≌△DCF;
(2)试证明:以A,F,D,E为顶点的四边形是平行四边形.
【答案】
(1)证明:如图,∵AB∥CD,
∴∠B=∠C.
∵在△ABE与△DCF中,
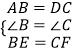 ,
,
∴△ABE≌△DCF(SAS)
(2)证明:如图,连接AF、DE.
由(1)知,△ABE≌△DCF,
∴AE=DF,∠AEB=∠DFC,
∴∠AEF=∠DFE,
∴AE∥DF,
∴以A、F、D、E为顶点的四边形是平行四边形.
【解析】(1)要证明△ABE≌△DCF,题中已知这两个三角形中两组对应边相等,还差一条件,要么证明第三组对应边相等,或证已知两组对应边的夹角相等,根据已知AB∥CD,可证得已知两组对应边的夹角相等,即可证明两三角形全等。
(2)根据(1)中易证得△ABE≌△DCF,可证明到AE平行且等于DF。继而可证得以A、F、D、E为顶点的四边形是平行四边形。


科目:初中数学 来源: 题型:
【题目】在一个不透明袋子中有1个红球和3个白球,这些球除颜色外都相同.
(1)从袋中任意摸出2个球,用树状图或列表求摸出的2个球颜色不同的概率;
(2)在袋子中再放入x个白球后,进行如下实验:从袋中随机摸出1个球,记录下颜色后放回袋子中并搅匀.经大量试验,发现摸到白球的频率稳定在0.95左右,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,点P是三角形内的任意一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为12,则PD+PE+PF=( )

A.8B.6C.4D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人分别从![]() ,
,![]() 两地相向而行,他们距
两地相向而行,他们距![]() 地的距离
地的距离![]() 与时间
与时间![]() 的关系如图所示,下列说法错误的是( )
的关系如图所示,下列说法错误的是( )

A.甲的速度是![]() B.甲出发4.5小时后与乙相遇
B.甲出发4.5小时后与乙相遇
C.乙比甲晚出发2小时D.乙的速度是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某生物兴趣小组在四天的试验研究中发现:骆驼的体温会随外部环境温度的变化而变化,而且在这四天中每昼夜的体温变化情况相同.他们将一头骆驼前两昼夜的体温变化情况绘制成如图所示的图象,请根据图象完成下列问题:
(1)第一天中,在什么时间范围内这头骆驼的体温是上升的?它的体温从最低上升到最高需要多长时间?
(2)第三天12时这头骆驼的体温是多少?
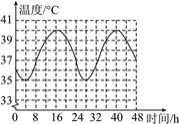
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
第1个等式:a1=![]() =
=![]() ×(
×(![]() ﹣
﹣![]() );
);
第2个等式:a2=![]() =
=![]() ×(
×(![]() ﹣
﹣![]() );
);
第3个等式:a3=![]() =
=![]() ×(
×(![]() );
);
第4个等式:a4=![]() =
=![]() ×(
×(![]() );
);
…
请解答下列问题:
(1)按以上规律列出第5个等式:a5= = ;第n(n为正整数)个等式:an= = ;
(2)求a1+a2+a3+a4+…+a100的值;
(3)数学符号![]() f(x)=f(1)+f(2)+f(3)+…+f(n),试求
f(x)=f(1)+f(2)+f(3)+…+f(n),试求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面的图表是我国数学家发明的“杨辉三角”,此图揭示了![]() (n为非负整数)的展开式的项数及各项系数的有关规律.请你观察,并根据此规律写出:
(n为非负整数)的展开式的项数及各项系数的有关规律.请你观察,并根据此规律写出:![]() _________.
_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 的方格中,每一个小方格的边长为1,点
的方格中,每一个小方格的边长为1,点![]() 在小方格的顶点上,请按下列要求分别画出一个以点
在小方格的顶点上,请按下列要求分别画出一个以点![]() 为顶点的四边形,且所画四边形的四个顶点都在小方格的顶点上.
为顶点的四边形,且所画四边形的四个顶点都在小方格的顶点上.

(1)在图①中画一个一般的平行四边形(非矩形或菱形),面积为6.
(2)在图②中画一个菱形或正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+b2﹣4ac与反比例函数y= ![]() 在同一坐标系内的图象大致为( )
在同一坐标系内的图象大致为( )
A.
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com