
【题目】如图,点A,B,C,D在一条直线上,△ABF≌△DCE.你能得出哪些结论?(请写出三个以上的结论)
【答案】解:∵△ABF≌△DCE
∴∠BAF=∠CDE,∠AFB=∠DEC,∠ABF=∠DCE,AB=DC,BF=CE,AF=DE;
∴AF∥ED,AC=BD,BF∥CE
【解析】根据全等三角形对应角相等,对应边相等得出∠BAF=∠CDE,∠AFB=∠DEC,∠ABF=∠DCE,AB=DC,BF=CE,AF=DE;再根据平行线的判定定理及等式的性质得出AF∥ED,AC=BD,BF∥CE。
【考点精析】掌握平行线的判定和全等三角形的性质是解答本题的根本,需要知道同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;全等三角形的对应边相等; 全等三角形的对应角相等.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】某商店取厂家选购甲、乙两种商品,乙商品每件进价比甲商品每件进价多20元,若购进甲商品5件和乙商品4件共需要800元;
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)若甲种商品的售价为每件100元,乙种商品的售价为每件125元,该商店准备购进甲、乙两种商品共40件,且这两种商品全部售出后总利润不少于900元,则甲种商品最多可购进多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按照有关规定,距高铁轨道![]() 米以内的区域内不宜临路新建学校、医院、敬老院和集中住宅区等噪声敏感建筑物.如图是一个小区平面示意图,长方形
米以内的区域内不宜临路新建学校、医院、敬老院和集中住宅区等噪声敏感建筑物.如图是一个小区平面示意图,长方形![]() 为一新建小区,直线
为一新建小区,直线![]() 为高铁轨道,
为高铁轨道,![]() 是直线
是直线![]() 上的两点,点
上的两点,点![]() 在一条直线上,且
在一条直线上,且![]() .小王看中了
.小王看中了![]() 号楼
号楼![]() 单元的一套住宅,与售楼人员的对话如下:
单元的一套住宅,与售楼人员的对话如下:
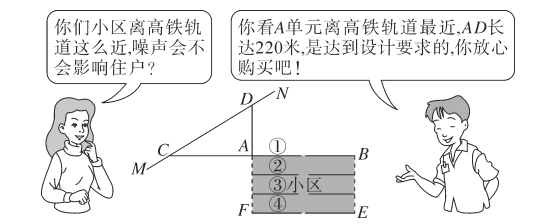
![]() 小王心中一算,发现售楼人员的话不可信,请你用所学的数学知识说明理由;
小王心中一算,发现售楼人员的话不可信,请你用所学的数学知识说明理由;
![]() 若一列长度为
若一列长度为![]() 米的高铁以
米的高铁以![]() 千米/时的速度通过,则
千米/时的速度通过,则![]() 单元用户受到影响的时间有多长?
单元用户受到影响的时间有多长?
(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O,A两处观测P处,仰角分别为α、β,且tanα= ![]() ,tan
,tan ![]() ,以O为原点,OA所在直线为x轴建立直角坐标系.
,以O为原点,OA所在直线为x轴建立直角坐标系.
(1)求点P的坐标;
(2)水面上升1m,水面宽多少( ![]() 取1.41,结果精确到0.1m)?
取1.41,结果精确到0.1m)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD和CEFG的边长分别为m、n,那么△AEG的面积的值( )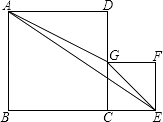
A.与m、n的大小都有关
B.与m、n的大小都无关
C.只与m的大小有关
D.只与n的大小有关
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
如图1,在△ABC中,AB=AC,射线BP从BA所在位置开始绕点B顺时针旋转,旋转角为α(0°<α<180°)
(1)当∠BAC=60°时,将BP旋转到图2位置,点D在射线BP上.若∠CDP=120°,则∠ACD∠ABD(填“>”、“=”、“<”),线段BD、CD与AD之间的数量关系是;
(2)当∠BAC=120°时,将BP旋转到图3位置,点D在射线BP上,若∠CDP=60°,求证:BD﹣CD= ![]() AD;
AD;
(3)将图3中的BP继续旋转,当30°<α<180°时,点D是直线BP上一点(点P不在线段BD上),若∠CDP=120°,请直接写出线段BD、CD与AD之间的数量关系(不必证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从1、2、3、4中任取一个数作为十位上的数字,再从余下的数字中任取一个数作为个位上的数字,那么组成的两位数是6的倍数的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )

A. 3 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() 的坐标为
的坐标为![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() ,且
,且![]() 为
为![]() 的中点,双曲线
的中点,双曲线![]() 经过
经过![]() 、
、![]() 两点.
两点.

(1)求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)如图1,点![]() 在
在![]() 轴上,若四边形
轴上,若四边形![]() 是平行四边形,求点
是平行四边形,求点![]() 的坐标;
的坐标;
(3)如图2,在(2)的条件下,动点![]() 在双曲线
在双曲线![]() 上,点
上,点![]() 在
在![]() 轴上,若以
轴上,若以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形,试求满足要求的所有点
为顶点的四边形为平行四边形,试求满足要求的所有点![]() 、
、![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com