
����Ŀ���ۺ���
��ͼ1���ڡ�ABC�У�AB=AC������BP��BA����λ�ÿ�ʼ�Ƶ�B˳ʱ����ת����ת��Ϊ����0�㣼����180�㣩
��1������BAC=60��ʱ����BP��ת��ͼ2λ�ã���D������BP�ϣ�����CDP=120�㣬���ACD��ABD�����������=���������������߶�BD��CD��AD֮���������ϵ����
��2������BAC=120��ʱ����BP��ת��ͼ3λ�ã���D������BP�ϣ�����CDP=60�㣬��֤��BD��CD= ![]() AD��
AD��
��3����ͼ3�е�BP������ת����30�㣼����180��ʱ����D��ֱ��BP��һ�㣨��P�����߶�BD�ϣ�������CDP=120�㣬��ֱ��д���߶�BD��CD��AD֮���������ϵ������֤������
���𰸡�
��1��=,BD=CD+AD
��2��֤������ͼ3����AC��BD�ཻ�ڵ�O����BP�Ͻ�ȡBE=CD������AE��
��A��AF��BD��F��

�ߡ�CDP=60�㣬
���CDB=120�㣮
�ߡ�CAB=120�㣬
���CDB=��CAB��
�ߡ�DOC=��AOB��
���DOC�ס�AOB��
���DCA=��EBA��
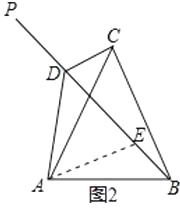
�ڡ�DCA���EBA�У�
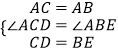 ��
��
���DCA�ա�EBA��SAS����
��AD=AE����DAC=��EAB��
�ߡ�CAB=��CAE+��EAB=120�㣬
���DAE=120�㣬
���ADE=��AED= ![]() =30�㣮
=30�㣮
����Rt��ADF�У���ADF=30�㣬
��DF= ![]() AD��
AD��
��DE=2DF= ![]() AD��
AD��
��BD=DE+BE= ![]() AD+CD��
AD+CD��
��BD��CD= ![]() AD
AD
��3���⣺�߶�BD��CD��AD֮���������ϵΪBD+CD= ![]() AD��CD��BD=
AD��CD��BD= ![]() AD
AD
���������⣺��1����ͼ2��
�ߡ�CDP=120�㣬
���CDB=60�㣬
�ߡ�BAC=60�㣬
���CDB=��BAC=60�㣬
��A��B��C��D�ĵ㹲Բ��
���ACD=��ABD��
��BP�Ͻ�ȡBE=CD������AE��
�ڡ�DCA���EBA�У�
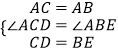 ��
��
���DCA�ա�EBA��SAS����
��AD=AE����DAC=��EAB��
�ߡ�CAB=��CAE+��EAB=60�㣬
���DAE=60�㣬
���ADE�ǵȱ������Σ�
��DE=AD��
��BD=BE+DE��
��BD=CD+AD��
���Դ���=��BD=CD+AD��
�����㾫��������Բ�ܽǶ��������������ε��ж��������ǽ����ĸ�������Ҫ֪��������Բ���ϵĽǽ���Բ�Ľ�;������Բ���ϣ����������߷ֱ���Բ����һ������Ľǽ���Բ�ܽ�;һ�������Ե�Բ�ܽǵ��������Ե�Բ�Ľǵ�һ�룻���������ε�һ�ж�Ӧ�߶�(��Ӧ�ߡ���Ӧ���ߡ���Ӧ��ƽ���ߡ����Բ�뾶������Բ�뾶�ȣ��ıȵ������Ʊȣ������������ܳ��ıȵ������Ʊȣ���������������ıȵ������Ʊȵ�ƽ����


 �ľ�ͼ���ʱ�ȷ�ϵ�д�
�ľ�ͼ���ʱ�ȷ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �ķ����У�ÿһ��С����ı߳�Ϊ1����
�ķ����У�ÿһ��С����ı߳�Ϊ1����![]() ��С����Ķ����ϣ��밴����Ҫ��ֱ�һ���Ե�
��С����Ķ����ϣ��밴����Ҫ��ֱ�һ���Ե�![]() Ϊ������ı��Σ��������ı��ε��ĸ����㶼��С����Ķ����ϣ�
Ϊ������ı��Σ��������ı��ε��ĸ����㶼��С����Ķ����ϣ�

��1����ͼ���л�һ��һ���ƽ���ı��Σ��Ǿ��λ����Σ������Ϊ6��
��2����ͼ���л�һ�����λ������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��ͼ����ͼ��ʾ����һ�κ���y=bx+b2��4ac�뷴��������y= ![]() ��ͬһ����ϵ�ڵ�ͼ�����Ϊ�� ��
��ͬһ����ϵ�ڵ�ͼ�����Ϊ�� ��
A.
B.
C.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ƽ��ֱ������ϵxOy�У������� ![]() ����A��6��0���͵�B��3��
����A��6��0���͵�B��3�� ![]() ����
����
��1����������y1�Ľ���ʽ��
��2����������y1��x�ᷭ�۵�������y2 �� ��������y2�Ľ���ʽ��
��3���ڣ�2���������£�������y2���Ƿ���ڵ�M��ʹ��OAM���AOB���ƣ�������ڣ������M�����ꣻ��������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B��C��D��һ��ֱ���ϣ���ABF�ա�DCE�����ܵó���Щ���ۣ�����д���������ϵĽ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ֱ���������ص���һ�𣬽�����һ�����������ŵ�B����C�ķ���ƽ�Ƶ���DEF��λ�ã�AB=a��DH=4��ƽ�ƾ���CFΪa-2������a�Ĵ���ʽ��ʾ��Ӱ���ֵ����____________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У�BC=a����BC�ߵ����ȷֵ�C1��ʹ��CC1��BC1=1��2������C1��AC��ƽ���߽�AB�ڵ�A1������A1��BC��ƽ���߽�AC�ڵ�D1����BC1�ߵ����ȷֵ�C2��ʹ��C1C2��BC2=1��2������C2��AC��ƽ���߽�AB�ڵ�A2������A2��BC��ƽ���߽�A1C1�ڵ�D2����˽�����ȥ�����߶�AnDn�ij���Ϊ______________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�У� ADΪ��BAC��ƽ���ߣ�AFΪBC���ϵĸߣ�
��1������B=38������C=76�������DAF�Ķ�����
��2������B=m������C=n������m<n�������DAF�Ķ������ú�m��n��ʽ�ӱ�ʾ����
��3������C-��B=30�������DAF=_________�ȣ�����գ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AEF��80�����ҡ�A��x�㣬��C��y�㣬��F��z�㣮��![]() ��|y��80��m|��|z��40|��0��mΪ��������0��m��100��
��|y��80��m|��|z��40|��0��m��������0��m��100��
(1) ���A����C�Ķ������ú�m�Ĵ���ʽ��ʾ��
(2) ��֤��AB��CD
(3) ����A��40�㣬��BAM��20�㣬��EFM��10����ֱ��AM��ֱ��FM���ڵ�M��ֱ��д����AMF�Ķ���


�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com