练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】两个直角三角形重叠在一起，将其中一个三角形沿着点B到点C的方向平移到△DEF的位置，AB=a，DH=4，平移距离CF为a-2，试用a的代数式表示阴影部分的面积____________．

    【答案】

    【解析】

    根据平移的性质，对应点间的距离等于平移距离可得BE的值； 再表示出EH，然后求出梯形ABEH的面积，再求出阴影部分的面积等于梯形ABEH的面积，从而得解．

    解：∵△ABC平移得到△DEF，

    ∴BE=CF=a-2；

    ∵AB=DE=a，DH=4，

    ∴EH=DE-DH=a-4，

    ∴梯形ABEH的面积=，

    阴影部分的面积=S△DEF-S△ECH=S△ABC-S△ECH=S梯形ABEH，

    所以，阴影部分的面积=．

    故答案为：．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，△OAB的顶点A在x轴正半轴上，OC是△OAB的中线，点B，C在反比例函数y= （x＞0）的图象上，若△OAB的面积等于6，则k的值为（ ）

    A.2
    B.4
    C.6
    D.8

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在直角坐标系中，△ABO的顶点坐标分别为O（0，0）、A（2a，0）、B（0，﹣a），线段EF两端点坐标为E（﹣m，a+1），F（﹣m，1）（2a＞m＞a）；直线l∥y轴交x轴于P（a，0），且线段EF与CD关于y轴对称，线段CD与NM关于直线l对称．

    （1）求点N、M的坐标（用含m、a的代数式表示）；

    （2）△ABO与△MFE通过平移能重合吗？能与不能都要说明其理由，若能请你说出一个平移方案（平移的单位数用m、a表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC 中，点 D 是边 BC 上的点（与 B、C 两点不重合），过点 D作 DE∥AC，DF∥AB，分别交 AB、AC 于 E、F 两点，下列说法正确的是（ ）

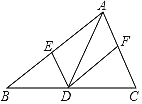
    A. 若 AD 平分∠BAC，则四边形 AEDF 是菱形

    B. 若 BD＝CD，则四边形 AEDF 是菱形

    C. 若 AD 垂直平分 BC，则四边形 AEDF 是矩形

    D. 若 AD⊥BC，则四边形 AEDF 是矩形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】综合题

    如图1，在△ABC中，AB=AC，射线BP从BA所在位置开始绕点B顺时针旋转，旋转角为α（0°＜α＜180°）
    （1）当∠BAC=60°时，将BP旋转到图2位置，点D在射线BP上．若∠CDP=120°，则∠ACD∠ABD（填“＞”、“=”、“＜”），线段BD、CD与AD之间的数量关系是；
    （2）当∠BAC=120°时，将BP旋转到图3位置，点D在射线BP上，若∠CDP=60°，求证：BD﹣CD= AD；
    （3）将图3中的BP继续旋转，当30°＜α＜180°时，点D是直线BP上一点（点P不在线段BD上），若∠CDP=120°，请直接写出线段BD、CD与AD之间的数量关系（不必证明）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在平行四边形ABCD中，EF过对角线的交点O，如果AB=6cm，AD=5cm，OF=2cm，那么四边形 BCEF的周长为________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了抓住梵净山文化艺术节的商机，某商店决定购进A、B两种艺术节纪念品．若购进A种纪念品8件，B种纪念品3件，需要950元；若购进A种纪念品5件，B种纪念品6件，需要800元．

    （1）求购进A、B两种纪念品每件各需多少元？

    （2）若该商店决定购进这两种纪念品共100件，考虑市场需求和资金周转，用于购买这100件纪念品的资金不少于7500元，但不超过7650元，那么该商店共有几种进货方案？

    （3）若销售每件A种纪念品可获利润20元，每件B种纪念品可获利润30元，在第（2）问的各种进货方案中，哪一种方案获利最大？最大利润是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AC是一棵大树，BF是一个斜坡，坡角为30°，某时刻太阳光直射斜坡BF，树顶端A的影子落到斜坡上的点D处，已知BC=6m，BD=4m，求树高AC的高度（结果精确到0.1m，参考数据： ≈1.414， ≈1.732）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校德育处组织“四品八德”好少年评比活动，每班只有一个名额．现某班有甲、乙、丙三名学生参与竞选，第一轮根据“品行规范”、“学习规范”进行量化考核．甲乙丙他们的量化考核成绩（单位：分）分别用两种方式进行了统计，如下表和图1：

    （1）请将表和图1中的空缺部分补充完整；

    （2）竞选的第二轮是由本班的50位学生进行投票，每票计6分，甲、乙、丙三人的得票情况如图2（没有弃权票，每名学生只能选一人）．

    ①若将“品行规范”、“学习规范”、“得票”三项测试得分按4:3:3的比例确定最后成绩，通过计算谁将会被推选为校“四品八德”好少年．

    ②若规定得票测试分占20％，要使甲学生最后得分不低于91分，则“品行规范”成绩在总分中所占比例的取值范围应是 ．

    查看答案和解析>>

    同步练习册答案