
【题目】已知:如图,在平面直角坐标系xOy中,抛物线 ![]() 过点A(6,0)和点B(3,
过点A(6,0)和点B(3, ![]() ).
).
(1)求抛物线y1的解析式;
(2)将抛物线y1沿x轴翻折得抛物线y2 , 求抛物线y2的解析式;
(3)在(2)的条件下,抛物线y2上是否存在点M,使△OAM与△AOB相似?如果存在,求出点M的坐标;如果不存在,说明理由.
【答案】
(1)解:依题意,得 ![]()
解得 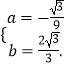 ,
,
∴抛物线y1的解析式为: ![]()
(2)解:将抛物线y1沿x轴翻折后,仍过点O(0,0),A(6,0),还过点B关于x轴的对称点 ![]() ,
,
设抛物线y2的解析式为: ![]() ,
,
∴ ![]() ,
,
解得: 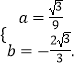
∴抛物线y2的解析式为 ![]()
(3)解:过点B作BC⊥x轴于点C,
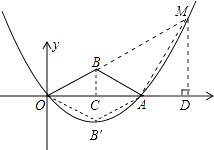
则有 ![]() .
.
∴∠BOC=30°,∠OBC=60°.
∵OC=3,OA=6,
∴AC=3.
∴∠BAC=30°,∠OBA=120°.
∴OB=AB.
即△OBA是顶角为120°的等腰三角形.
分两种情况:
①当点M在x轴下方时,△OAM就是△OAB',此时点M的坐标为 ![]() .
.
②当点M在x轴上方时,假设△OAM∽△OBA,
则有AM=OA=6,∠OAM=120°.
过点M作MD⊥x轴于点D,则∠MAD=60°.
∴ ![]() ,AD=3.∴OD=9.
,AD=3.∴OD=9.
而(9, ![]() )满足关系式
)满足关系式 ![]() ,
,
即点M在抛物线 ![]() 上.
上.
根据对称性可知,点 ![]() 也满足条件.
也满足条件.
综上所述,点M的坐标为 ![]() ,
, ![]() ,
, ![]() .
.
【解析】(1)分别将A、B两点的坐标代入抛物线 y 1 = a x 2 + b x,用待定系数法求解;(2)将抛物线y1沿x轴翻折后,仍过点O,A,还过点B关于x轴的对称点 B ',设抛物线y2的解析式为: y 2 = m x 2 + n x ,用待定系数法即可求解;(3)①当点M在x轴下方时,△OAM就是△OAB,'②当点M在x轴上方时,假设△OAM∽△OBA,分别得出M点的坐标即可。


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=150°,AC=4,tanB= ![]() .
.
(1)求BC的长;
(2)利用此图形求tan15°的值(精确到0.1,参考数据: ![]() =1.4,
=1.4, ![]() =1.7,
=1.7, ![]() =2.2)
=2.2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD折叠,使点C与A点重合,折痕为EF.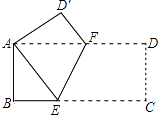
(1)判断四边形AFCE的形状,并说明理由.
(2)若AB=4,BC=8,求折痕EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,△ABO的顶点坐标分别为O(0,0)、A(2a,0)、B(0,﹣a),线段EF两端点坐标为E(﹣m,a+1),F(﹣m,1)(2a>m>a);直线l∥y轴交x轴于P(a,0),且线段EF与CD关于y轴对称,线段CD与NM关于直线l对称.
(1)求点N、M的坐标(用含m、a的代数式表示);
(2)△ABO与△MFE通过平移能重合吗?能与不能都要说明其理由,若能请你说出一个平移方案(平移的单位数用m、a表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O,A两处观测P处,仰角分别为α、β,且tanα= ![]() ,tan
,tan ![]() ,以O为原点,OA所在直线为x轴建立直角坐标系.
,以O为原点,OA所在直线为x轴建立直角坐标系.
(1)求点P的坐标;
(2)水面上升1m,水面宽多少( ![]() 取1.41,结果精确到0.1m)?
取1.41,结果精确到0.1m)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,点 D 是边 BC 上的点(与 B、C 两点不重合),过点 D作 DE∥AC,DF∥AB,分别交 AB、AC 于 E、F 两点,下列说法正确的是( )
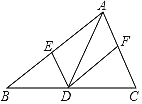
A. 若 AD 平分∠BAC,则四边形 AEDF 是菱形
B. 若 BD=CD,则四边形 AEDF 是菱形
C. 若 AD 垂直平分 BC,则四边形 AEDF 是矩形
D. 若 AD⊥BC,则四边形 AEDF 是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
如图1,在△ABC中,AB=AC,射线BP从BA所在位置开始绕点B顺时针旋转,旋转角为α(0°<α<180°)
(1)当∠BAC=60°时,将BP旋转到图2位置,点D在射线BP上.若∠CDP=120°,则∠ACD∠ABD(填“>”、“=”、“<”),线段BD、CD与AD之间的数量关系是;
(2)当∠BAC=120°时,将BP旋转到图3位置,点D在射线BP上,若∠CDP=60°,求证:BD﹣CD= ![]() AD;
AD;
(3)将图3中的BP继续旋转,当30°<α<180°时,点D是直线BP上一点(点P不在线段BD上),若∠CDP=120°,请直接写出线段BD、CD与AD之间的数量关系(不必证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了抓住梵净山文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠C=90°,BC=8厘米,点D在AC上,CD=3厘米.点P、Q分别由A,C两点同时出发,点P沿AC方向向点C匀速移动,速度为每秒k厘米,行完AC全程用时8秒;点Q沿CB方向向点B匀速移动,速度为每秒1厘米.设运动的时间为x秒(0<x<8),△DCQ的面积为y1平方厘米,△PCQ的面积为y2平方厘米.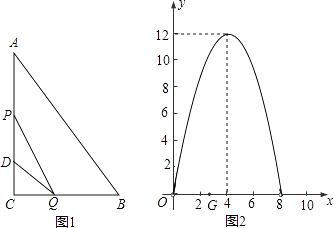
(1)求y1与x的函数关系,并在图2中画出y1的图象;
(2)如图2,y2的图象是抛物线的一部分,其顶点坐标是(4,12),求点P的速度及AC的长;
(3)在图2中,点G是x轴正半轴上一点0<OG<6,过G作EF垂直于x轴,分别交y1、y2的图象于点E、F.
①说出线段EF的长在图1中所表示的实际意义;
②当0<x<6时,求线段EF长的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com