
【题目】△ABC中, AD为∠BAC的平分线,AF为BC边上的高.
(1)若∠B=38°,∠C=76°,求∠DAF的度数.
(2)若∠B=m°,∠C=n°,(m<n).求∠DAF的度数(用含m、n的式子表示).
(3)若∠C-∠B=30°,则∠DAF=_________度.(填空)

【答案】(1)19°;(2)![]() ;(3)15°
;(3)15°
【解析】
(1)由三角形的内角和是180°,可求∠BAC=66°,因为AD为∠BAC的平分线,得∠BAD=33°;又由三角形的一个外角等于与它不相邻的两个内角的和,得∠ADC=∠BAD+∠B=71°;又已知AF为BC边上的高,所以∠DAF=90°-∠ADC=19°;
(2)求出∠BAC度数,求出∠DAC,根据角平分线求出∠BAD,根据三角形外角的性质求出∠ADC的度数,即可求出∠DAF度数;
(3)利用(2)的结论即可求出答案.
解:(1)∵∠BAC+∠B+∠C=180°,
又∵∠B=38°,∠C=76°,
∴∠BAC=66°.
∵AD为∠BAC的平分线,
∴∠BAD=33°,
∴∠ADC=∠BAD+∠B=71°.
又∵AF为BC边上的高,
∴∠DAF=90°-∠ADC=19°.
(2)∵∠BAC+∠B+∠C=180°,
又∵∠B=m°,∠C=n°,
∴∠BAC=180°- m°-n°.
∵AD为∠BAC的平分线,
∴∠BAD=![]() ,
,
∴∠ADC=∠BAD+∠B=![]()
又∵AF为BC边上的高,
∴∠DAF=90°-∠ADC=![]() .
.
(3)由(2)可知∠DAF=90°-∠ADC=![]()
∵∠C-∠B=30°
∴∠DAF=15°
故答案为:15°


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD折叠,使点C与A点重合,折痕为EF.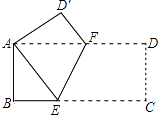
(1)判断四边形AFCE的形状,并说明理由.
(2)若AB=4,BC=8,求折痕EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
如图1,在△ABC中,AB=AC,射线BP从BA所在位置开始绕点B顺时针旋转,旋转角为α(0°<α<180°)
(1)当∠BAC=60°时,将BP旋转到图2位置,点D在射线BP上.若∠CDP=120°,则∠ACD∠ABD(填“>”、“=”、“<”),线段BD、CD与AD之间的数量关系是;
(2)当∠BAC=120°时,将BP旋转到图3位置,点D在射线BP上,若∠CDP=60°,求证:BD﹣CD= ![]() AD;
AD;
(3)将图3中的BP继续旋转,当30°<α<180°时,点D是直线BP上一点(点P不在线段BD上),若∠CDP=120°,请直接写出线段BD、CD与AD之间的数量关系(不必证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了抓住梵净山文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )

A. 3 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是一棵大树,BF是一个斜坡,坡角为30°,某时刻太阳光直射斜坡BF,树顶端A的影子落到斜坡上的点D处,已知BC=6m,BD=4m,求树高AC的高度(结果精确到0.1m,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.

(1)如图1,直接写出∠A和∠C之间的数量关系___;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E. F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠C=90°,BC=8厘米,点D在AC上,CD=3厘米.点P、Q分别由A,C两点同时出发,点P沿AC方向向点C匀速移动,速度为每秒k厘米,行完AC全程用时8秒;点Q沿CB方向向点B匀速移动,速度为每秒1厘米.设运动的时间为x秒(0<x<8),△DCQ的面积为y1平方厘米,△PCQ的面积为y2平方厘米.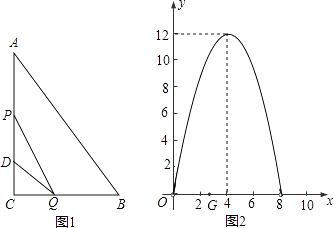
(1)求y1与x的函数关系,并在图2中画出y1的图象;
(2)如图2,y2的图象是抛物线的一部分,其顶点坐标是(4,12),求点P的速度及AC的长;
(3)在图2中,点G是x轴正半轴上一点0<OG<6,过G作EF垂直于x轴,分别交y1、y2的图象于点E、F.
①说出线段EF的长在图1中所表示的实际意义;
②当0<x<6时,求线段EF长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A.不可能事件发生的概率为0
B.随机事件发生的概率为 ![]()
C.概率很小的事件不可能发生
D.投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com