练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示，在△ABC中，AE、BF是角平分线，它们相交于点O，AD是高，∠BAC=50°，∠C=70°，求∠DAE，∠AOB的度数．

    【答案】∠DAE=5°，∠AOB=125°．

    【解析】

    ∠DAE=∠BAD-∠BAE，根据题意分别求出∠BAD和∠BAE的度数求解即可；先求出∠BAE、∠ABF的度数，在△ABO中根据三角形内角和定理，求∠AOB的度数即可.

    解：在△ABC中，

    ∵∠BAC=50°，∠C=70°，

    ∴∠ABC=60°，

    ∴∠BAD=30°，

    又∵AE平分∠BAC，

    ∴∠BAE=∠BAC=25°，

    ∴∠DAE=∠BAD-∠BAE=30°-25°=5°；

    ∵BF平分∠ABC，

    ∴∠ABF=∠ABC=30°，

    ∴∠AOB=180°-∠BAE-∠ABF=180°-25°-30°=125°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】（1）阅读理解：

    如图①，在△ABC中，若AB=8，AC=4，求BC边上的中线AD的取值范围是　 　

    （2）问题解决：如图②，在△ABC中D是BC边上的中点，DE⊥DF于点D，DE交AB于点E，DF交AC于点F，连接EF，求证：BE+CF＞EF；

    （3）问题拓展：如图③，在四边形ABCD中，∠B+∠D=180°，CB=CD，∠BCD=140°，以C为顶点作一个70角的两边分别交AB，AD于E，F两点，连接EF，探索线段BE，DF，EF之间的数量关系，并加以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，CE平分∠ACD，AE平分∠BAC，∠EAC+∠ACE=90°．

    （1）请判断AB与CD的位置关系，并说明理由；

    （2）如图2，在（1）的结论下，当∠E=90°保持不变，移动直角顶点E，使∠MCE=∠ECD．当直角顶点E点移动时，问∠BAE与∠MCD是否存在确定的数量关系？并说明理由；

    （3）如图3，在（1）的结论下，P为线段AC上一定点，点Q为直线CD上一动点，当点Q在射线CD上运动时（点C除外），∠CPQ+∠CQP与∠BAC有何数量关系？直接写出结论，其数量关系为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在数轴上点A，点B对应的数分别是6，﹣6，∠DCE＝90°（点C与点O重合，点D在数轴的正半轴上）

    （1）如图1，若CF平分∠ACE，则∠AOF＝　 　度；点A与点B的距离=　

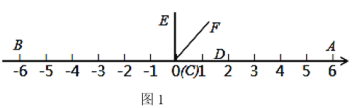
    （2）如图2，将∠DCE沿数轴的正半轴向右平移t（0＜t＜3）个单位后，再绕点顶点C逆时针旋转30t度，作CF平分∠ACE，此时记∠DCF＝α．

    ①当t＝1时，α＝　 　；点B与点C的距离=　

    ②猜想∠BCE和α的数量关系，并说明理由；

    （3）如图3，开始∠D1C1E1与∠DCE重合，将∠DCE沿数轴的正半轴向右平移t（0t3）个单位，再绕点顶点C逆时针旋转30t度，作CF平分∠ACE，此时记∠DCF＝α，与此同时，将∠D1C1E1沿数轴的负半轴向左平移t（0t3）个单位，再绕点顶点C1顺时针旋转30t度，作C1F1平分∠AC1E1，记∠D1C1F1＝β，若α与β满足|α﹣β|＝20°，求t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个盒子里有标号分别为1，2，3，4，5，6的六个小球，这些小球除标号数字外都相同．
    （1）从盒中随机摸出一个小球，求摸到标号数字为奇数的小球的概率；
    （2）甲、乙两人用这六个小球玩摸球游戏，规则是：甲从盒中随机摸出一个小球，记下标号数字后放回盒里，充分摇匀后，乙再从盒中随机摸出一个小球，并记下标号数字．若两次摸到小球的标号数字同为奇数或同为偶数，则判甲赢；若两次摸到小球的标号数字为一奇一偶，则判乙赢．请用列表法或画树状图的方法说明这个游戏对甲、乙两人是否公平．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

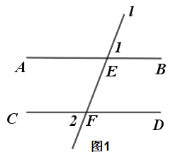
    【题目】已知：直线l分别交AB、CD与E、F两点，且AB∥CD．

    （1） 说明：∠1=∠2；

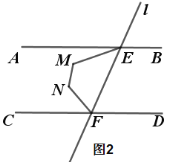
    （2） 如图2，点M、N在AB、CD之间，且在直线l左侧，若∠EMN+∠FNM=260°，

    ①求：∠AEM+∠CFN的度数；

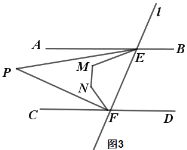
    ②如图3，若EP平分∠AEM，FP平分∠CFN，求∠P的度数；

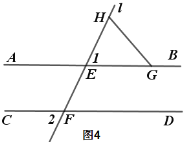
    （3） 如图4，∠2=80°，点G在射线EB上，点H在AB上方的直线l上，点Q是平面内一点，连接QG、QH，若∠AGQ=18°，∠FHQ=24°，直接写出∠GQH的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，等腰△ABC底边BC的长为4cm，面积为12cm，腰AB的垂直平分线交AB于点E，若点D为BC边的中点，M为线段EF上一动点，则△BDM的周长最小值为_________

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：（ ﹣2）0+（ ）﹣1﹣2cos30°﹣| ﹣2|

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】中点、平行线、等腰直角三角形、等边三角形都是常见的几何图形！
    （1）如图1，若点D为等腰直角三角形ABC斜边BC的中点，点E，F分别在AB、AC边上，且∠EDF=90°，连接AD、EF，当BC=5 ，FC=2时，求EF的长度；

    （2）如图2，若点D为等边三角形ABC边BC的中点，点E，F分别在AB，AC边上，且∠EDF=90°；M为EF的中点，连接CM，当DF∥AB时，证明：3ED=2MC；

    （3）如图3，若点D为等边三角形ABC边BC的中点，点E，F分别在AB，AC边上，且∠EDF=90°；当BE=6，CF=0.8时，直接写出EF的长度．

    查看答案和解析>>

    同步练习册答案