
【题目】如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°.
(1)请判断AB与CD的位置关系,并说明理由;
(2)如图2,在(1)的结论下,当∠E=90°保持不变,移动直角顶点E,使∠MCE=∠ECD.当直角顶点E点移动时,问∠BAE与∠MCD是否存在确定的数量关系?并说明理由;
(3)如图3,在(1)的结论下,P为线段AC上一定点,点Q为直线CD上一动点,当点Q在射线CD上运动时(点C除外),∠CPQ+∠CQP与∠BAC有何数量关系?直接写出结论,其数量关系为 .

【答案】(1)平行,理由见解析(2)∠BAE+![]() ∠MCD=90°,理由见解析(3)∠BAC=∠CPQ+∠CQP
∠MCD=90°,理由见解析(3)∠BAC=∠CPQ+∠CQP
【解析】
(1)由角平分线的性质得出∠BAC=2∠EAC,∠ACD=2∠ACE,推出∠BAC+∠ACD=180°,即可得出结论;
(2)过E作EF∥AB,则EF∥AB∥CD,得出∠BAE=∠AEF,∠FEC=∠DCE,由∠AEC=90°,推出∠BAE+∠ECD=90°,∠ECD=![]() ∠MCD,得出∠BAE+
∠MCD,得出∠BAE+![]() ∠MCD=90°;
∠MCD=90°;
(3)由平行线的性质得出∠BAC+∠ACD=180°,由三角形内角和定理得出∠CPQ+∠CQP+∠PCQ=180°,即可得出结果.
(1)AB∥CD;理由如下:
∵CE平分∠ACD,AE平分∠BAC,
∴∠BAC=2∠EAC,∠ACD=2∠ACE,
∵∠EAC+∠ACE=90°,
∴∠BAC+∠ACD=180°,
∴AB∥CD;
(2)∠BAE+![]() ∠MCD=90°;理由如下:
∠MCD=90°;理由如下:
过E作EF∥AB,如图2所示:
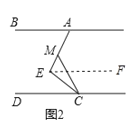
∵AB∥CD,
∴EF∥AB∥CD,
∴∠BAE=∠AEF,∠FEC=∠DCE,
∵∠AEC=90°,
∴∠BAE+∠ECD=90°,
∵∠MCE=∠ECD
∴∠ECD=![]() ∠MCD
∠MCD
∴∠BAE+![]() ∠MCD=90°;
∠MCD=90°;
(3)∠BAC=∠CPQ+∠CQP;理由如下:
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵∠CPQ+∠CQP+∠PCQ=180°,
即(∠CPQ+∠CQP)+∠ACD=180°,
∴∠BAC=∠CPQ+∠CQP.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】为了抓住梵净山文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠C=90°,BC=8厘米,点D在AC上,CD=3厘米.点P、Q分别由A,C两点同时出发,点P沿AC方向向点C匀速移动,速度为每秒k厘米,行完AC全程用时8秒;点Q沿CB方向向点B匀速移动,速度为每秒1厘米.设运动的时间为x秒(0<x<8),△DCQ的面积为y1平方厘米,△PCQ的面积为y2平方厘米.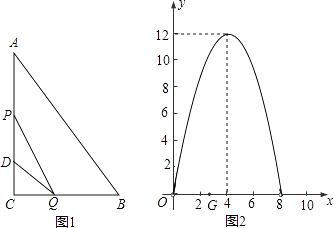
(1)求y1与x的函数关系,并在图2中画出y1的图象;
(2)如图2,y2的图象是抛物线的一部分,其顶点坐标是(4,12),求点P的速度及AC的长;
(3)在图2中,点G是x轴正半轴上一点0<OG<6,过G作EF垂直于x轴,分别交y1、y2的图象于点E、F.
①说出线段EF的长在图1中所表示的实际意义;
②当0<x<6时,求线段EF长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校德育处组织“四品八德”好少年评比活动,每班只有一个名额.现某班有甲、乙、丙三名学生参与竞选,第一轮根据“品行规范”、“学习规范”进行量化考核.甲乙丙他们的量化考核成绩(单位:分)分别用两种方式进行了统计,如下表和图1:


(1)请将表和图1中的空缺部分补充完整;
(2)竞选的第二轮是由本班的50位学生进行投票,每票计6分,甲、乙、丙三人的得票情况如图2(没有弃权票,每名学生只能选一人).
①若将“品行规范”、“学习规范”、“得票”三项测试得分按4:3:3的比例确定最后成绩,通过计算谁将会被推选为校“四品八德”好少年.
②若规定得票测试分占20%,要使甲学生最后得分不低于91分,则“品行规范”成绩在总分中所占比例的取值范围应是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,有以下结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的结论有_____个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年疫情期间,某公司为了扩大经营,决定购进6台机器用于生产口罩.现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产口罩的数量如下表所示.经过预算,本次购买机器所耗资金不能超过36万元,
(1)按该公司要求可以有几种购买方案?
(2)如果该公司购进的6台机器的日生产能力不能低于42万个,那么为了节约资金应选择什么样的购买方案?
甲 | 乙 | |
价格(万元/台) | 7 | 5 |
每台日产量(万个) | 10 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A.不可能事件发生的概率为0
B.随机事件发生的概率为 ![]()
C.概率很小的事件不可能发生
D.投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△![]() 中,∠ACB=90°,∠ABC与∠BAC的角平分线相交于点P,连接CP,过点P作DE⊥CP分别交AC、BC于点D、E,
中,∠ACB=90°,∠ABC与∠BAC的角平分线相交于点P,连接CP,过点P作DE⊥CP分别交AC、BC于点D、E,

(1)若∠BAC=40°,求∠APB与∠ADP度数;
(2)探究:通过(1)的计算,小明猜测∠APB=∠ADP,请你说明小明猜测的正确性(要求写出过程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com