
【题目】2020年疫情期间,某公司为了扩大经营,决定购进6台机器用于生产口罩.现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产口罩的数量如下表所示.经过预算,本次购买机器所耗资金不能超过36万元,
(1)按该公司要求可以有几种购买方案?
(2)如果该公司购进的6台机器的日生产能力不能低于42万个,那么为了节约资金应选择什么样的购买方案?
甲 | 乙 | |
价格(万元/台) | 7 | 5 |
每台日产量(万个) | 10 | 6 |
【答案】(1)有4种购买方案①购甲0台,购乙6台,②购甲1台,购乙5台,③购甲2台,购乙4台④购甲3台,购乙3台;(2)购买甲种机器2台,购买乙种机器4台
【解析】
(1)购甲x台,则购乙(6-x)台,根据“本次购买机器所耗资金不能超过36万元”列出一元一次不等式,即可求出x的取值范围,从而求出结论;
(2)购甲x台,则购乙(6-x)台,根据“本次购买机器所耗资金不能超过36万元且该公司购进的6台机器的日生产能力不能低于42万个”列出一元一次不等式组,即可求出x的取值范围,从而求出结论;
解:(1)购甲x台,则购乙(6-x)台
由题意可得7x+5(6-x)≤36
解得:x≤3
所以x=0或1或2或3
当x=0时,6-x=6;
当x=1时,6-x=5;
当x=2时,6-x=4;
当x=3时,6-x=3;
答:有4种购买方案①购甲0台,购乙6台,②购甲1台,购乙5台,③购甲2台,购乙4台④购甲3台,购乙3台;
(2)购甲x台,则购乙(6-x)台
由题意可得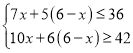
解得:![]()
∴x=2或3
当x=2时,购买机器所耗资金为7×2+5×(6-2)=34(万元);
当x=3时,购买机器所耗资金为7×3+5×(6-3)=36(万元)
∵34万元<36万元
∴购甲2台,购乙6-2=4台所耗资金最少
答:为了节约资金应购买甲种机器2台,购买乙种机器4台.


 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.

(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:平面直角坐标系中,A(a,3)、B(b,6)、C(c,1),a、b、c都为实数,并且满足3b-5c=-2a-18,4b-c=3a+10
(1) 请直接用含a的代数式表示b和c
(2) 当实数a变化时,判断△ABC的面积是否发生变化?若不变,求其值;若变化,求其变化范围
(3) 当实数a变化时,若线段AB与y轴相交,线段OB与线段AC交于点P,且S△PAB>S△PBC,求实数a的取值范围.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°.
(1)请判断AB与CD的位置关系,并说明理由;
(2)如图2,在(1)的结论下,当∠E=90°保持不变,移动直角顶点E,使∠MCE=∠ECD.当直角顶点E点移动时,问∠BAE与∠MCD是否存在确定的数量关系?并说明理由;
(3)如图3,在(1)的结论下,P为线段AC上一定点,点Q为直线CD上一动点,当点Q在射线CD上运动时(点C除外),∠CPQ+∠CQP与∠BAC有何数量关系?直接写出结论,其数量关系为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有依次排列的三个数:“![]() ,
,![]() ,
,![]() ”对这三个数作如下操作:对任何相邻的两个数,都用左边的数减去右边的数,将所得之差写在这两个数之间,即可产生一个新数串:“2,7,-5,-13,8”称为第一次操作;做第二次同样的操作后又产生一个新数串:“2,-5,7,12,-5,8,-13,-21,8”……依次继续操作下去,直到第
”对这三个数作如下操作:对任何相邻的两个数,都用左边的数减去右边的数,将所得之差写在这两个数之间,即可产生一个新数串:“2,7,-5,-13,8”称为第一次操作;做第二次同样的操作后又产生一个新数串:“2,-5,7,12,-5,8,-13,-21,8”……依次继续操作下去,直到第![]() 次操作后停止操作.则第
次操作后停止操作.则第![]() 次操作所得新数串中所有各数的和为_____.
次操作所得新数串中所有各数的和为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在数轴上点A,点B对应的数分别是6,﹣6,∠DCE=90°(点C与点O重合,点D在数轴的正半轴上)
(1)如图1,若CF平分∠ACE,则∠AOF= 度;点A与点B的距离=
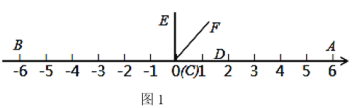
(2)如图2,将∠DCE沿数轴的正半轴向右平移t(0<t<3)个单位后,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α.

①当t=1时,α= ;点B与点C的距离=
②猜想∠BCE和α的数量关系,并说明理由;
(3)如图3,开始∠D1C1E1与∠DCE重合,将∠DCE沿数轴的正半轴向右平移t(0![]() t
t![]() 3)个单位,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α,与此同时,将∠D1C1E1沿数轴的负半轴向左平移t(0
3)个单位,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α,与此同时,将∠D1C1E1沿数轴的负半轴向左平移t(0![]() t
t![]() 3)个单位,再绕点顶点C1顺时针旋转30t度,作C1F1平分∠AC1E1,记∠D1C1F1=β,若α与β满足|α﹣β|=20°,求t的值.
3)个单位,再绕点顶点C1顺时针旋转30t度,作C1F1平分∠AC1E1,记∠D1C1F1=β,若α与β满足|α﹣β|=20°,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
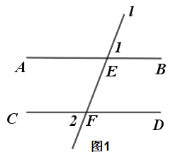
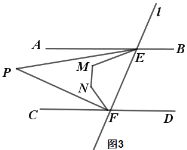
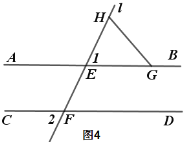
【题目】已知:直线l分别交AB、CD与E、F两点,且AB∥CD.
(1) 说明:∠1=∠2;
(2) 如图2,点M、N在AB、CD之间,且在直线l左侧,若∠EMN+∠FNM=260°,
①求:∠AEM+∠CFN的度数;
②如图3,若EP平分∠AEM,FP平分∠CFN,求∠P的度数;
(3) 如图4,∠2=80°,点G在射线EB上,点H在AB上方的直线l上,点Q是平面内一点,连接QG、QH,若∠AGQ=18°,∠FHQ=24°,直接写出∠GQH的度数.
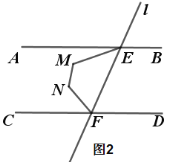
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF.
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为3,∠EAC=60°,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com