Question

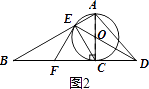
【题目】已知如图，以Rt△ABC的AC边为直径作⊙O交斜边AB于点E，连接EO并延长交BC的延长线于点D，点F为BC的中点，连接EF．

（1）求证：EF是⊙O的切线；
（2）若⊙O的半径为3，∠EAC=60°，求AD的长．

Answer 1

【答案】
（1）解：如图1，连接FO，

∵F为BC的中点，AO=CO，

∴OF∥AB，

∵AC是⊙O的直径，

∴CE⊥AE，

∵OF∥AB，

∴OF⊥CE，

∴OF所在直线垂直平分CE，

∴FC=FE，OE=OC，

∴∠FEC=∠FCE，∠0EC=∠0CE，

∵∠ACB=90°，

即：∠0CE+∠FCE=90°，

∴∠0EC+∠FEC=90°，

即：∠FEO=90°，

∴FE为⊙O的切线；

（2）解：如图2，

∵⊙O的半径为3，

∴AO=CO=EO=3，

∵∠EAC=60°，OA=OE，
∴△AOE是等边三角形，

∴∠EOA=60°

∴∠COD=∠EOA=60°，

∵在Rt△OCD中，∠COD=60°，OC=3，

∴CD= ，

∵在Rt△ACD中，∠ACD=90°，

CD= ，AC=6，

∴AD= ．

【解析】（1）由已知可知，添加辅助线连接FO，易证OF是△ABC的中位线，得到OF∥AB，又有AC是⊙O的直径，证得OF垂直平分EC。根据垂直平分线的性质及等角的余角相等得到∠FEO=90°，从而得到结论。或证△OEF和△OFC，即可得出结论。
（2）根据已知条件易证得△AOE是等边三角形，得出∠COD=∠EOA=60°，在Rt△OCD中求出CD的长，再在Rt△ACD中根据勾股定理求出AD的长即可。
【考点精析】根据题目的已知条件，利用线段垂直平分线的判定和含30度角的直角三角形的相关知识可以得到问题的答案，需要掌握和一条线段两个端点距离相等的点，在这条线段的垂直平分线上；在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半．