
【题目】已知△ABC中,AB=AC,点D,E分别在直线AB,AC上,且∠DEC=∠DCE
(1)如图1,点D在线段AB上∠A=90°,若等腰直角三角形的边与斜边之比为![]() ,求证:
,求证:![]()
(2)如图2,若点D在线段AB的延长线上,∠A=60°,求证:EB=AD

【答案】(1)见解析;(2)见解析
【解析】
(1)过D点作BC的平行线交AC于点G,先证△DBE≌△CGD,再证△ADG是等腰直角三角形即可;
(2)过D点作BC的平行线交AC的延长线于点F,先证△ABC和△ADF是等边三角形,再证△DBE≌△CGD即可.
证明:过D点作BC的平行线交AC于点G,
∵△ABC是等腰三角形,∠A=90°,
∴∠ABC=∠ACB=45°,
∴∠DBE=180°-45°=135°,
∵DG∥BC,
∴∠GDC=∠DCE,∠DGC=180°-45°=135°,
∴∠DBE=∠DGC,
∵∠DCE=∠DEC,
∴ED=CD,∠DEC=∠GDC,
在△DBE和△CGD中

∴△DBE≌△CGD(AAS),
∴BE=GD,
∵∠ADG=∠ABC=45°,∠A=90°,
∴△ADG是等腰直角三角形,
∴DG=![]() AD,
AD,
∴BE=![]() AD;
AD;
(2)证明:过D点作BC的平行线交AC的延长线于点F,

∵△ABC是等腰三角形,∠A=60°,
∴△ABC是等边三角形.
∴∠ABC=60°,
∵DF∥BC,
∴∠ADF=∠ABC=60°,
∴△ADF是等边三角形,
∴AD=DF,∠AFD=60°,
∵∠DBE=∠ABC=60°,
∴∠DBE=∠AFD,
∵∠FDC=∠DCE,∠DCE=∠DEC,
∴∠FDC=∠DEC,ED=CD,
在△DBE和△CFD中

∴△DBE≌△CGD(AAS)
∴BE=DF,
∴BE=AD.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】有依次排列的三个数:“![]() ,
,![]() ,
,![]() ”对这三个数作如下操作:对任何相邻的两个数,都用左边的数减去右边的数,将所得之差写在这两个数之间,即可产生一个新数串:“2,7,-5,-13,8”称为第一次操作;做第二次同样的操作后又产生一个新数串:“2,-5,7,12,-5,8,-13,-21,8”……依次继续操作下去,直到第
”对这三个数作如下操作:对任何相邻的两个数,都用左边的数减去右边的数,将所得之差写在这两个数之间,即可产生一个新数串:“2,7,-5,-13,8”称为第一次操作;做第二次同样的操作后又产生一个新数串:“2,-5,7,12,-5,8,-13,-21,8”……依次继续操作下去,直到第![]() 次操作后停止操作.则第
次操作后停止操作.则第![]() 次操作所得新数串中所有各数的和为_____.
次操作所得新数串中所有各数的和为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+2x+3与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,连接BC.
(1)求A,B,C三点的坐标;
(2)若点P为线段BC上一点(不与B,C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当△BCM的面积最大时,求△BPN的周长;
(3)在(2)的条件下,当△BCM的面积最大时,在抛物线的对称轴上存在一点Q,使得△CNQ为直角三角形,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块长为![]() 米,宽为
米,宽为![]() 米的长方形空地,计划修筑东西、南北走向的两条道路,其余进行绿化(阴影部分),已知道路宽为
米的长方形空地,计划修筑东西、南北走向的两条道路,其余进行绿化(阴影部分),已知道路宽为![]() 米,东西走向的道路与空地北边界相距1米,则绿化的面积是多少平方米?并求出当a=3,b=2时的绿化面积.
米,东西走向的道路与空地北边界相距1米,则绿化的面积是多少平方米?并求出当a=3,b=2时的绿化面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF.
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为3,∠EAC=60°,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价为120元、170元的A,B两种型号的电风扇,如表所示是近2周的销售情况:(进价、售价均保持不变,利润=销售收入一进货成本)
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 6 | 5 | 2200元 |
第二周 | 4 | 10 | 3200元 |
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市再采购这两种型号的电风扇共130台,并且全部销售完,该超市能否实现这两批的总利润为8010元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题 1、化简
2、若一次函数y=kx+b经过点A(3,4)、B(4,5),求这一次函数的解析式.
(1)先化简,再求值: ![]() ÷(2+
÷(2+ ![]() )
)
(2)若一次函数y=kx+b经过点A(3,4)、B(4,5),求这一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
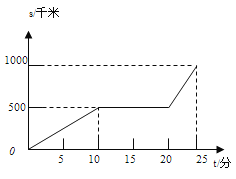
【题目】某天早晨,王老师从家出发步行前往学校,途中在路边一饭店吃早餐,如图所示是王老师从家到学校这一过程中所走的路程S(米)与时间t(分)之间的关系.
(1)学校离他家 米,从出发到学校,王老师共用了 分钟;
(2)王老师吃早餐用了多少分钟?
(3)王老师吃早餐以前的速度快还是吃完早餐以后的速度快?吃完早餐后的平均速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,CD⊥AB于D,在(1)DCAB=ACBC;(2)![]() ;(3)
;(3)![]() ;(4)AC+BC>CD+AB中正确的个数是( )
;(4)AC+BC>CD+AB中正确的个数是( )

![]()
A.4B.3C.2D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com