
【题目】计算题 1、化简
2、若一次函数y=kx+b经过点A(3,4)、B(4,5),求这一次函数的解析式.
(1)先化简,再求值: ![]() ÷(2+
÷(2+ ![]() )
)
(2)若一次函数y=kx+b经过点A(3,4)、B(4,5),求这一次函数的解析式.
【答案】
(1)解: ![]() ÷(2+
÷(2+ ![]() )
)
= ![]()
= ![]()
= ![]() ;
;
(2)解:∵一次函数y=kx+b的图象经过点A(3,4)和点B(4,5),
∴ ![]() ,
,
解得: ![]() ,
,
∴一次函数解析式为y=x+1
【解析】(1)先将括号里面通分,分子分母能分解因式的先分解因式,再把除法运算转化为乘法运算,结果化成最简分式。
(2)将A、B两点坐标分别代入函数解析式,建立二元一次方程组,求解即可。
【考点精析】本题主要考查了分式的混合运算和确定一次函数的表达式的相关知识点,需要掌握运算的顺序:第一级运算是加法和减法;第二级运算是乘法和除法;第三级运算是乘方.如果一个式子里含有几级运算,那么先做第三级运算,再作第二级运算,最后再做第一级运算;如果有括号先做括号里面的运算.如顺口溜:"先三后二再做一,有了括号先做里."当有多层括号时,先算括号内的运算,从里向外{[(?)]};确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法才能正确解答此题.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图①、图②,在给定的一张矩形纸片上作一个正方形,甲、乙两人的作法如下:
甲:以点A为圆心,AD长为半径画弧,交AB于点E,以点D为圆心,AD长为半径画弧,交CD于点F,连接EF,则四边形AEFD即为所求;
乙:作∠DAB的平分线,交CD于点M,同理作∠ADC的平分线,交AB于点N,连接MN,则四边形ADMN即为所求.


对于以上两种作法,可以做出的判定是( )
A.甲正确,乙错误B.甲、乙均正确
C.乙正确,甲错误D.甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用两种方法证明“四边形的外角和等于360°”.
如图,∠DAE、∠ABF、∠BCG、∠CDH是四边形ABCD的四个外角.
求证:∠DAE+∠ABF+∠BCG+∠CDH=360°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC,点D,E分别在直线AB,AC上,且∠DEC=∠DCE
(1)如图1,点D在线段AB上∠A=90°,若等腰直角三角形的边与斜边之比为![]() ,求证:
,求证:![]()
(2)如图2,若点D在线段AB的延长线上,∠A=60°,求证:EB=AD

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用完全平方公式因式分解在数学中的应用,请回答下列问题:
(1)因式分解:![]() _______.
_______.
(2)填空:
①当![]() 时,代数式
时,代数式![]() _______.
_______.
②当![]() _______时,代数式
_______时,代数式![]() ;
;
③代数式![]() 的最小值是_______.
的最小值是_______.
(3)拓展与应用:当![]() 、
、![]() 为何值时,代数式
为何值时,代数式![]() 有最小值,并求出这个最小值.
有最小值,并求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、 乙两家超市以相同的价格出售同样的商品.为了吸引顾客,各自推出不同的优惠方案: 在甲超市累计购买商品超出 300 元之后,超出部分按原价八折优惠;在乙超市累计购买商品超出 200 元之后,超出部分按原价九折优惠.设顾客预计累计购物 ![]() 元(
元( ![]() 300)
300)
(1)请用x 的代数式分别表示顾客在两家超市购物所付的费用;
(2)试比较顾客到哪家超市购物更优惠? 说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从热气球C处测得地面A,B两点的俯角分别是30°、45°,如果此时热气球C处的高度CD为100米,点A,D,B在同一直线上,则AB两点的距离是( )
A.200米
B.200 ![]() 米
米
C.220 ![]() 米
米
D.100( ![]() )米
)米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了进一步了解七年级800名学生的身体素质情况,体育老师抽取七年级男女各25位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如下所示:
组别 | 次数x | 频数(人数) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 |
|
第4组 | 140≤x<160 | 16 |
第5组 | 160≤x<180 | 6 |

请结合图表完成下列问题:
(1)表中的![]() ,跳绳次数低于140次的有
,跳绳次数低于140次的有![]() 人,则
人,则![]()
(2)请把频数分布直方图补充完整;
(3)若七年级学生一分钟跳绳次数(x)达标要求是:x≥120.请估算七年级学生达标人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数 ![]() 的图象经过点(
的图象经过点( ![]() ,8),直线y=﹣x+b经过该反比例函数图象上的点Q(4,m).
,8),直线y=﹣x+b经过该反比例函数图象上的点Q(4,m).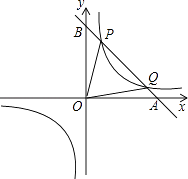
(1)求上述反比例函数和直线的函数表达式;
(2)设该直线与x轴、y轴分别相交于A、B两点,与反比例函数图象的另一个交点为P,连接0P、OQ,求△OPQ的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com