
【题目】如图,已知抛物线y=﹣x2+2x+3与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,连接BC.
(1)求A,B,C三点的坐标;
(2)若点P为线段BC上一点(不与B,C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当△BCM的面积最大时,求△BPN的周长;
(3)在(2)的条件下,当△BCM的面积最大时,在抛物线的对称轴上存在一点Q,使得△CNQ为直角三角形,求点Q的坐标.
【答案】
(1)解:由抛物线的解析式y=﹣x2+2x+3,
∴C(0,3),
令y=0,﹣x2+2x+3=0,解得x=3或x=﹣1;
∴A(﹣1,0),B(3,0).
(2)解:设直线BC的解析式为:y=kx+b,则有:
![]() ,解得
,解得 ![]() ,
,
∴直线BC的解析式为:y=﹣x+3.
设P(x,﹣x+3),则M(x,﹣x2+2x+3),
∴PM=(﹣x2+2x+3)﹣(﹣x+3)=﹣x2+3x.
∴S△BCM=S△PMC+S△PMB= ![]() PM(xP﹣xC)+
PM(xP﹣xC)+ ![]() PM(xB﹣xP)=
PM(xB﹣xP)= ![]() PM(xB﹣xC)=
PM(xB﹣xC)= ![]() PM.
PM.
∴S△BCM= ![]() (﹣x2+3x)=﹣
(﹣x2+3x)=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() .
.
∴当x= ![]() 时,△BCM的面积最大.
时,△BCM的面积最大.
此时P( ![]() ,
, ![]() ),∴PN=ON=
),∴PN=ON= ![]() ,
,
∴BN=OB﹣ON=3﹣ ![]() =
= ![]() .
.
在Rt△BPN中,由勾股定理得:PB= ![]() .
.
C△BCN=BN+PN+PB=3+ ![]() .
.
∴当△BCM的面积最大时,△BPN的周长为3+ ![]()
(3)解:∵y=﹣x2+2x+3=﹣(x﹣1)2+4
∴抛物线的对称轴为直线x=1.
在Rt△CNO中,OC=3,ON= ![]() ,由勾股定理得:CN=
,由勾股定理得:CN= ![]() .
.
设点D为CN中点,则D( ![]() ,
, ![]() ),CD=ND=
),CD=ND= ![]() .
.
如解答图,△CNQ为直角三角形,
①若点Q为直角顶点.
作Rt△CNO的外接圆⊙D,与对称轴交于Q1、Q2两点,由圆周角定理可知,Q1、Q2两点符合题意.
连接Q1D,则Q1D=CD=ND= ![]() .
.
过点D( ![]() ,
, ![]() )作对称轴的垂线,垂足为E,
)作对称轴的垂线,垂足为E,
则E(1, ![]() ),Q1E=Q2E,DE=1﹣
),Q1E=Q2E,DE=1﹣ ![]() =
= ![]() .
.
在Rt△Q1DE中,由勾股定理得:
Q1E= ![]() =
= ![]() .
.
∴Q1(1, ![]() ),Q2(1,
),Q2(1, ![]() );
);
②若点N为直角顶点.
过点N作NF⊥CN,交对称轴于点Q3,交y轴于点F.
易证Rt△NFO∽Rt△CNO,则 ![]() =
= ![]() ,即
,即 ![]() ,解得OF=
,解得OF= ![]() .
.
∴F(0,﹣ ![]() ),又∵N(
),又∵N( ![]() ,0),
,0),
∴可求得直线FN的解析式为:y= ![]() x﹣
x﹣ ![]() .
.
当x=1时,y=﹣ ![]() ,
,
∴Q3(1,﹣ ![]() );
);
③当点C为直角顶点时.
过点C作Q4C⊥CN,交对称轴于点Q4.
∵Q4C∥FN,∴可设直线Q4C的解析式为:y= ![]() x+b,
x+b,
∵点C(0,3)在该直线上,∴b=3.
∴直线Q4C的解析式为:y= ![]() x+3,
x+3,
当x=1时,y= ![]() ,
,
∴Q4(1, ![]() ).
).
综上所述,满足条件的点Q有4个,
其坐标分别为:Q1(1, ![]() ),Q2(1,
),Q2(1, ![]() ),Q3(1,﹣
),Q3(1,﹣ ![]() ),Q4(1,
),Q4(1, ![]() ).
).

【解析】(1)根据函数解析式由x=0求出点C的坐标,由y=0,求出点A、B的坐标。
(2)先求出直线BC的函数解析式,抓住PM∥y轴,设出点P、M的坐标(点P、M的横坐标相同),就可以求出S△BCM与x的函数解析式,即可求出点P的坐标,再求出PN、BP、BN的长,即可求出△BPN的周长。
(3)在Rt△CON中,利用勾股定理可求出CN的长,再求出CN的中点D的坐标,然后分类讨论:①若点Q为直角顶点.②若点N为直角顶点.③当点C为直角顶点时.运用勾股定理、相似三角形的性质和判定、一次函数等相关知识进行解答。


科目:初中数学 来源: 题型:
【题目】如图,已知∠A=∠D,有下列五个条件:①AE=DE,②BE=CE,③AB=DC,④∠ABC=∠DCB,⑤AC=BD,能证明△ABC与△DCB全等的条件有几个?并选择其中一个进行证明.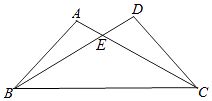
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①、图②,在给定的一张矩形纸片上作一个正方形,甲、乙两人的作法如下:
甲:以点A为圆心,AD长为半径画弧,交AB于点E,以点D为圆心,AD长为半径画弧,交CD于点F,连接EF,则四边形AEFD即为所求;
乙:作∠DAB的平分线,交CD于点M,同理作∠ADC的平分线,交AB于点N,连接MN,则四边形ADMN即为所求.


对于以上两种作法,可以做出的判定是( )
A.甲正确,乙错误B.甲、乙均正确
C.乙正确,甲错误D.甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O,A在数轴上表示的数分别是0,l,将线段OA分成1000等份,其分点由左向右依次为M1,M2…M999;将线段OM1分成1000等份,其分点由左向右依次为N1,N2…N999;将线段ON1分成1000等份,其分点由左向右依次为P1,P2…P999.则点P314所表示的数用科学记数法表示为_____.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC边上一点,AB=DB,BE平分∠ABC,交AC于点E,连接DE.
(1)求证:△ABE≌△DBE;
(2)若∠A=100°,∠C=50°,求∠AEB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用两种方法证明“四边形的外角和等于360°”.
如图,∠DAE、∠ABF、∠BCG、∠CDH是四边形ABCD的四个外角.
求证:∠DAE+∠ABF+∠BCG+∠CDH=360°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC,点D,E分别在直线AB,AC上,且∠DEC=∠DCE
(1)如图1,点D在线段AB上∠A=90°,若等腰直角三角形的边与斜边之比为![]() ,求证:
,求证:![]()
(2)如图2,若点D在线段AB的延长线上,∠A=60°,求证:EB=AD

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了进一步了解七年级800名学生的身体素质情况,体育老师抽取七年级男女各25位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如下所示:
组别 | 次数x | 频数(人数) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 |
|
第4组 | 140≤x<160 | 16 |
第5组 | 160≤x<180 | 6 |

请结合图表完成下列问题:
(1)表中的![]() ,跳绳次数低于140次的有
,跳绳次数低于140次的有![]() 人,则
人,则![]()
(2)请把频数分布直方图补充完整;
(3)若七年级学生一分钟跳绳次数(x)达标要求是:x≥120.请估算七年级学生达标人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com