
【题目】如图,点O,A在数轴上表示的数分别是0,l,将线段OA分成1000等份,其分点由左向右依次为M1,M2…M999;将线段OM1分成1000等份,其分点由左向右依次为N1,N2…N999;将线段ON1分成1000等份,其分点由左向右依次为P1,P2…P999.则点P314所表示的数用科学记数法表示为_____.
![]()
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,则∠A、∠C、∠E、∠F满足的数量关系是( )

A. ∠A=∠C+∠E+∠F B. ∠A+∠E﹣∠C﹣∠F=180°
C. ∠A﹣∠E+∠C+∠F=90° D. ∠A+∠E+∠C+∠F=360°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有依次排列的三个数:“![]() ,
,![]() ,
,![]() ”对这三个数作如下操作:对任何相邻的两个数,都用左边的数减去右边的数,将所得之差写在这两个数之间,即可产生一个新数串:“2,7,-5,-13,8”称为第一次操作;做第二次同样的操作后又产生一个新数串:“2,-5,7,12,-5,8,-13,-21,8”……依次继续操作下去,直到第
”对这三个数作如下操作:对任何相邻的两个数,都用左边的数减去右边的数,将所得之差写在这两个数之间,即可产生一个新数串:“2,7,-5,-13,8”称为第一次操作;做第二次同样的操作后又产生一个新数串:“2,-5,7,12,-5,8,-13,-21,8”……依次继续操作下去,直到第![]() 次操作后停止操作.则第
次操作后停止操作.则第![]() 次操作所得新数串中所有各数的和为_____.
次操作所得新数串中所有各数的和为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年年初,我国爆发新冠肺炎疫情,某省邻近县市 C、D 获知 A、B 两市分别急需救援物资 200吨和 300 吨的消息后,决定调运物资支援.已知 C 市有救援物资 240 吨,D 市有救援物资 260 吨,现将这些救援物资全部调往 A、B 两市.已知从 C 市运往 A、B 两市的费用分别为每吨 20 元和 25 元,从D 市运往往 A、B 两市的费用分别为每吨 15 元和 30 元,设从 C 市运往 A 市的救援物资为 x 吨.
(1) 请填写下表;
A | B | 合计(吨) | |
C | x | _____ | 240 |
D | _____ | _____ | 260 |
总计(吨) | 200 | 300 | 500 |
(2)设 C、D 两市的总运费为 W 元,则 W 与 x 之间的函数关系式为_________,其中自变量 x的取值范围是________;
(3)经过抢修,从 C 市到 B 市的路况得到了改善,缩短了运输时间,运费每吨减少 n 元(n>10),其余路线运费不变,若 C、D 两市的总运费的最小值不小于 7920 元,则 n 的取值范围是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
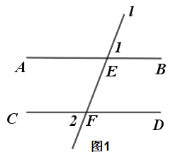
【题目】已知:直线l分别交AB、CD与E、F两点,且AB∥CD.
(1) 说明:∠1=∠2;
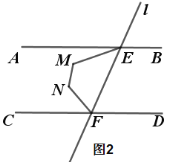
(2) 如图2,点M、N在AB、CD之间,且在直线l左侧,若∠EMN+∠FNM=260°,
①求:∠AEM+∠CFN的度数;
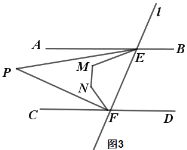
②如图3,若EP平分∠AEM,FP平分∠CFN,求∠P的度数;
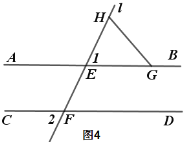
(3) 如图4,∠2=80°,点G在射线EB上,点H在AB上方的直线l上,点Q是平面内一点,连接QG、QH,若∠AGQ=18°,∠FHQ=24°,直接写出∠GQH的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
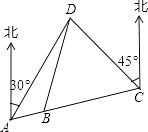
【题目】某市开展一项自行车旅游活动,线路需经A,B,C,D四地,如图,其中A,B,C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+2x+3与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,连接BC.
(1)求A,B,C三点的坐标;
(2)若点P为线段BC上一点(不与B,C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当△BCM的面积最大时,求△BPN的周长;
(3)在(2)的条件下,当△BCM的面积最大时,在抛物线的对称轴上存在一点Q,使得△CNQ为直角三角形,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块长为![]() 米,宽为
米,宽为![]() 米的长方形空地,计划修筑东西、南北走向的两条道路,其余进行绿化(阴影部分),已知道路宽为
米的长方形空地,计划修筑东西、南北走向的两条道路,其余进行绿化(阴影部分),已知道路宽为![]() 米,东西走向的道路与空地北边界相距1米,则绿化的面积是多少平方米?并求出当a=3,b=2时的绿化面积.
米,东西走向的道路与空地北边界相距1米,则绿化的面积是多少平方米?并求出当a=3,b=2时的绿化面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
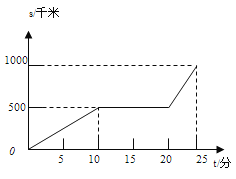
【题目】某天早晨,王老师从家出发步行前往学校,途中在路边一饭店吃早餐,如图所示是王老师从家到学校这一过程中所走的路程S(米)与时间t(分)之间的关系.
(1)学校离他家 米,从出发到学校,王老师共用了 分钟;
(2)王老师吃早餐用了多少分钟?
(3)王老师吃早餐以前的速度快还是吃完早餐以后的速度快?吃完早餐后的平均速度是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com