
【题目】有依次排列的三个数:“![]() ,
,![]() ,
,![]() ”对这三个数作如下操作:对任何相邻的两个数,都用左边的数减去右边的数,将所得之差写在这两个数之间,即可产生一个新数串:“2,7,-5,-13,8”称为第一次操作;做第二次同样的操作后又产生一个新数串:“2,-5,7,12,-5,8,-13,-21,8”……依次继续操作下去,直到第
”对这三个数作如下操作:对任何相邻的两个数,都用左边的数减去右边的数,将所得之差写在这两个数之间,即可产生一个新数串:“2,7,-5,-13,8”称为第一次操作;做第二次同样的操作后又产生一个新数串:“2,-5,7,12,-5,8,-13,-21,8”……依次继续操作下去,直到第![]() 次操作后停止操作.则第
次操作后停止操作.则第![]() 次操作所得新数串中所有各数的和为_____.
次操作所得新数串中所有各数的和为_____.
【答案】-12115
【解析】
根据题意分别计算出第1次、第2次、第3次操作后增加的和,发现每次操作后和均增加-6,进而推出规律,求出第![]() 次操作所得新数串中所有各数的和.
次操作所得新数串中所有各数的和.
解:第1次操作后增加数字:7,-13,
第1次操作后增加的和为:7+(-13)=-6;
第2次操作后增加数字:-5,12,8,-21,
第2次操作后增加的和为:-5+12+8+(-21)=-6;
第3次操作后增加数字:7,-12,-5,17,-13,21,8,-29,
第3次操作后增加的和为:7+(-12)+(-5)+17+(-13)+21+8+(-29)=-6;
……,
即每次操作后和增加-6,
∴第![]() 次操作后和增加2020×(-6)=-12120,
次操作后和增加2020×(-6)=-12120,
∴第![]() 次操作所得新数串中所有各数的和为2+(-5)+8+(-12120)=-12115.
次操作所得新数串中所有各数的和为2+(-5)+8+(-12120)=-12115.
故答案为:-12115.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】一个零件如图所示

(1)请说明∠BDC >∠A
(2)按规定∠A等于90°,∠B和∠C应分别等于32°和21°,检验工人量得∠BDC等于148°,就断定这个零件不合格,这是为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠A=∠D,有下列五个条件:①AE=DE,②BE=CE,③AB=DC,④∠ABC=∠DCB,⑤AC=BD,能证明△ABC与△DCB全等的条件有几个?并选择其中一个进行证明.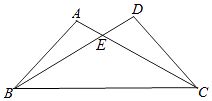
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年疫情期间,某公司为了扩大经营,决定购进6台机器用于生产口罩.现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产口罩的数量如下表所示.经过预算,本次购买机器所耗资金不能超过36万元,
(1)按该公司要求可以有几种购买方案?
(2)如果该公司购进的6台机器的日生产能力不能低于42万个,那么为了节约资金应选择什么样的购买方案?
甲 | 乙 | |
价格(万元/台) | 7 | 5 |
每台日产量(万个) | 10 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为5,P为⊙O上一点,P(4,3),PC、PD为⊙O的弦,分别交y轴正半轴于E、F,且PE=PF,连CD,设直线CD为y=kx+b,则k= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①、图②,在给定的一张矩形纸片上作一个正方形,甲、乙两人的作法如下:
甲:以点A为圆心,AD长为半径画弧,交AB于点E,以点D为圆心,AD长为半径画弧,交CD于点F,连接EF,则四边形AEFD即为所求;
乙:作∠DAB的平分线,交CD于点M,同理作∠ADC的平分线,交AB于点N,连接MN,则四边形ADMN即为所求.


对于以上两种作法,可以做出的判定是( )
A.甲正确,乙错误B.甲、乙均正确
C.乙正确,甲错误D.甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O,A在数轴上表示的数分别是0,l,将线段OA分成1000等份,其分点由左向右依次为M1,M2…M999;将线段OM1分成1000等份,其分点由左向右依次为N1,N2…N999;将线段ON1分成1000等份,其分点由左向右依次为P1,P2…P999.则点P314所表示的数用科学记数法表示为_____.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC,点D,E分别在直线AB,AC上,且∠DEC=∠DCE
(1)如图1,点D在线段AB上∠A=90°,若等腰直角三角形的边与斜边之比为![]() ,求证:
,求证:![]()
(2)如图2,若点D在线段AB的延长线上,∠A=60°,求证:EB=AD

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com