
【题目】如图,⊙O的半径为5,P为⊙O上一点,P(4,3),PC、PD为⊙O的弦,分别交y轴正半轴于E、F,且PE=PF,连CD,设直线CD为y=kx+b,则k= . 
【答案】![]()
【解析】解:
如图,取点P关于y轴的对称点Q,
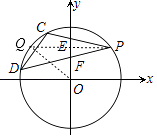
∵P(4,3),
∴Q(﹣4,3),连接PQ,
∴PQ⊥y轴,
∵PE=PF,
∴∠CPE=∠DPE,
∴点Q为 ![]() 的中点,
的中点,
连接OQ,则OQ⊥DC,
设直线OQ解析式为y=mx,
把Q点坐标代入可得3=﹣4m,解得m=﹣ ![]() ,
,
∴直线OQ解析式为y=﹣ ![]() x,
x,
∴直线CD解析式为y= ![]() x+b,
x+b,
∴k= ![]() ,
,
所以答案是: ![]() .
.
【考点精析】利用确定一次函数的表达式和垂径定理对题目进行判断即可得到答案,需要熟知确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图所示,点P在∠AOB内,点M、N分别是点P关于AO、BO所在直线的对称点.
(1)若△PEF的周长为20,求MN的长.
(2)若∠O=50°,求∠EPF的度数.
(3)请直接写出∠EPF与∠O的数量关系是_____________________________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,四边形
为坐标原点,四边形![]() 是矩形,点
是矩形,点![]() 的坐标分别为
的坐标分别为![]() ,点
,点![]() 以
以![]() 的速度从
的速度从![]() 出发向终点
出发向终点![]() 运动,点
运动,点![]() 以
以![]() 的速度从
的速度从![]() 出发向终点
出发向终点![]() 运动,当
运动,当![]() 是以
是以![]() 为一腰的等腰三角形时,点
为一腰的等腰三角形时,点![]() 的坐标为____.
的坐标为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=∠C=45°,点D在BC边上,点E在AC边上,且∠ADE=∠AED,连结DE.
(1)当∠BAD=60°,求∠CDE的度数;
(2)当点D在BC(点B、C除外)边上运动时,试写出∠BAD与∠CDE的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有依次排列的三个数:“![]() ,
,![]() ,
,![]() ”对这三个数作如下操作:对任何相邻的两个数,都用左边的数减去右边的数,将所得之差写在这两个数之间,即可产生一个新数串:“2,7,-5,-13,8”称为第一次操作;做第二次同样的操作后又产生一个新数串:“2,-5,7,12,-5,8,-13,-21,8”……依次继续操作下去,直到第
”对这三个数作如下操作:对任何相邻的两个数,都用左边的数减去右边的数,将所得之差写在这两个数之间,即可产生一个新数串:“2,7,-5,-13,8”称为第一次操作;做第二次同样的操作后又产生一个新数串:“2,-5,7,12,-5,8,-13,-21,8”……依次继续操作下去,直到第![]() 次操作后停止操作.则第
次操作后停止操作.则第![]() 次操作所得新数串中所有各数的和为_____.
次操作所得新数串中所有各数的和为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年年初,我国爆发新冠肺炎疫情,某省邻近县市 C、D 获知 A、B 两市分别急需救援物资 200吨和 300 吨的消息后,决定调运物资支援.已知 C 市有救援物资 240 吨,D 市有救援物资 260 吨,现将这些救援物资全部调往 A、B 两市.已知从 C 市运往 A、B 两市的费用分别为每吨 20 元和 25 元,从D 市运往往 A、B 两市的费用分别为每吨 15 元和 30 元,设从 C 市运往 A 市的救援物资为 x 吨.
(1) 请填写下表;
A | B | 合计(吨) | |
C | x | _____ | 240 |
D | _____ | _____ | 260 |
总计(吨) | 200 | 300 | 500 |
(2)设 C、D 两市的总运费为 W 元,则 W 与 x 之间的函数关系式为_________,其中自变量 x的取值范围是________;
(3)经过抢修,从 C 市到 B 市的路况得到了改善,缩短了运输时间,运费每吨减少 n 元(n>10),其余路线运费不变,若 C、D 两市的总运费的最小值不小于 7920 元,则 n 的取值范围是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
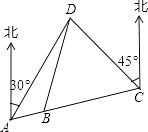
【题目】某市开展一项自行车旅游活动,线路需经A,B,C,D四地,如图,其中A,B,C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价为120元、170元的A,B两种型号的电风扇,如表所示是近2周的销售情况:(进价、售价均保持不变,利润=销售收入一进货成本)
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 6 | 5 | 2200元 |
第二周 | 4 | 10 | 3200元 |
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市再采购这两种型号的电风扇共130台,并且全部销售完,该超市能否实现这两批的总利润为8010元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com