
【题目】如图,已知∠A=∠D,有下列五个条件:①AE=DE,②BE=CE,③AB=DC,④∠ABC=∠DCB,⑤AC=BD,能证明△ABC与△DCB全等的条件有几个?并选择其中一个进行证明.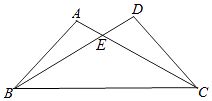
【答案】解:共5个:①或②或③或④或⑤.
若选①AE=DE,则证明如下:
在△ABE和△DCE中,
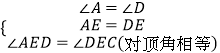 ,
,
∴AB=DC,BE=CE,
∴DE+BE=AE+CE,
∴BD=AC,
在△ABC和△DCB中,
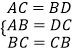 ,
,
∴△ABC≌△DCB(SSS);
若选②BE=CE,则证明如下:
证明:∵BE=CE
∴∠EBC=∠ECB,
在△ABC与△DCB中:
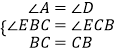 ,
,
∴△ABC≌△DCB(AAS);
若选③AB=DC,则证明如下:
在△ABE和△DCE中,
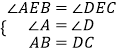 ,
,
∴△ABE≌△DCE(AAS),
∴BE=CE,
∴∠EBC=∠ECB,
在△ABC与△DCB中:
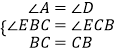 ,
,
∴△ABC≌△DCB(AAS);
若选④∠ABC=∠DCB,则证明如下:
证明:在△ABC与△DCB中:
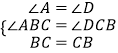 ,
,
∴△ABC≌△DCB(AAS);
若选⑤AC=BD,则证明如下:
如图,延长BA,CD交于点F,
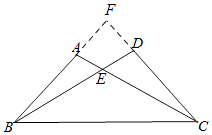
∵∠BAC=∠CDB,
∴∠FAC=∠FDB,
又∵∠F=∠F,BD=CA,
∴△BDF≌△CAF,
∴BF=CF,AF=DF,
∴AB=CD,
在△ABE和△DCE中,
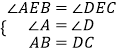 ,
,
∴△ABE≌△DCE(AAS),
∴BE=CE,
∴∠EBC=∠ECB,
在△ABC与△DCB中:
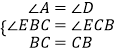 ,
,
∴△ABC≌△DCB(AAS).
综上所述,能证明△ABC与△DCB全等的条件有5个.
【解析】若已知两边对应相等,则找它们的夹角或第三边,若已知两角对应相等,则必须再找一组对边对应相等,若已知一边一角对应相等,则找令一组角,或找这个角得令一组对应邻边。


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注.某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请根据统计图中所提供的信息解答下列问题:
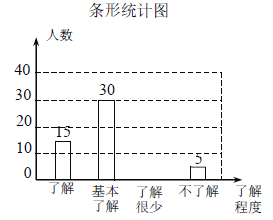
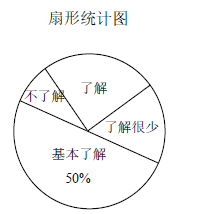
(1)接受问卷调查的学生共有 人;
(2)扇形统计图中“了解”部分所对应扇形的圆心角为 度;
(3)请补全条形统计图;
(4)若该中学共有学生1200人,则该中学学生对校园安全知识达到“了解”和“基本了解”程度的总人数约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,则∠A、∠C、∠E、∠F满足的数量关系是( )

A. ∠A=∠C+∠E+∠F B. ∠A+∠E﹣∠C﹣∠F=180°
C. ∠A﹣∠E+∠C+∠F=90° D. ∠A+∠E+∠C+∠F=360°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,四边形
为坐标原点,四边形![]() 是矩形,点
是矩形,点![]() 的坐标分别为
的坐标分别为![]() ,点
,点![]() 以
以![]() 的速度从
的速度从![]() 出发向终点
出发向终点![]() 运动,点
运动,点![]() 以
以![]() 的速度从
的速度从![]() 出发向终点
出发向终点![]() 运动,当
运动,当![]() 是以
是以![]() 为一腰的等腰三角形时,点
为一腰的等腰三角形时,点![]() 的坐标为____.
的坐标为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:平面直角坐标系中,A(a,3)、B(b,6)、C(c,1),a、b、c都为实数,并且满足3b-5c=-2a-18,4b-c=3a+10
(1) 请直接用含a的代数式表示b和c
(2) 当实数a变化时,判断△ABC的面积是否发生变化?若不变,求其值;若变化,求其变化范围
(3) 当实数a变化时,若线段AB与y轴相交,线段OB与线段AC交于点P,且S△PAB>S△PBC,求实数a的取值范围.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有依次排列的三个数:“![]() ,
,![]() ,
,![]() ”对这三个数作如下操作:对任何相邻的两个数,都用左边的数减去右边的数,将所得之差写在这两个数之间,即可产生一个新数串:“2,7,-5,-13,8”称为第一次操作;做第二次同样的操作后又产生一个新数串:“2,-5,7,12,-5,8,-13,-21,8”……依次继续操作下去,直到第
”对这三个数作如下操作:对任何相邻的两个数,都用左边的数减去右边的数,将所得之差写在这两个数之间,即可产生一个新数串:“2,7,-5,-13,8”称为第一次操作;做第二次同样的操作后又产生一个新数串:“2,-5,7,12,-5,8,-13,-21,8”……依次继续操作下去,直到第![]() 次操作后停止操作.则第
次操作后停止操作.则第![]() 次操作所得新数串中所有各数的和为_____.
次操作所得新数串中所有各数的和为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+2x+3与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,连接BC.
(1)求A,B,C三点的坐标;
(2)若点P为线段BC上一点(不与B,C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当△BCM的面积最大时,求△BPN的周长;
(3)在(2)的条件下,当△BCM的面积最大时,在抛物线的对称轴上存在一点Q,使得△CNQ为直角三角形,求点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com