
����Ŀ��ijУΪ�˽ⱾУѧ��ÿ�ܲμӿ��⸨������������������˲���ѧ��һ���ڲμӿ��⸨�����ѧ�������������������Ƴ���ͼ1��ͼ2��ʾ������������ͳ��ͼ������A��0��ѧ�ƣ�B��1��ѧ�ƣ�C��2��ѧ�ƣ�D��3��ѧ�ƣ�E��4��ѧ�ƻ����ϣ��������ͳ��ͼ�е���Ϣ������������⣺
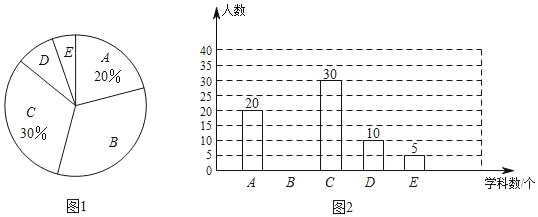
��1���뽫ͼ2��ͳ��ͼ����������
��2�����ݱ��ε�������ݣ�ÿ�ܲμӿ��⸨�����ѧ�������������� ����ѧ�ƣ�
��3������У����2000��ѧ�����������ϵ��������Ƹ�Уȫ��ѧ��һ���ڲμӿ��⸨������3��ѧ�ƣ���3��ѧ�ƣ����ϵ�ѧ�������� ���ˣ�
���𰸡���1��ͼ�μ���������2��1����3��300.
��������
��1����A������������ռ�ٷֱ��������������������ȥ��������������B���������ɲ�ȫͼ�Σ�
��2�����������Ķ������ɵã�
��3��������������������D��E����ռ�������ı������ɵã�
�⣺��1���߱������������Ϊ20��20%��100���ˣ���
��1��ѧ�ƣ�B��𣩵�����Ϊ100����20+30+10+5����35���ˣ���
��ȫͼ�����£�
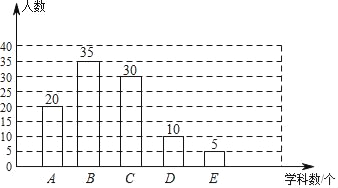
��2�����ݱ��ε�������ݣ�ÿ�ܲμӿ��⸨�����ѧ������������1��ѧ�ƣ�
�ʴ�Ϊ1��
��3�����Ƹ�Уȫ��ѧ��һ���ڲμӿ��⸨������3��ѧ�ƣ���3��ѧ�ƣ����ϵ�ѧ������2000��![]() ��300���ˣ���
��300���ˣ���
�ʴ�Ϊ300��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧΪ�˽�ѧ�������š����������֡�����������ӽ�Ŀ��ϲ�������������ͳ�Ƶ���![]() ���������ij������ͬѧ��ϲ���Ľ�Ŀ
���������ij������ͬѧ��ϲ���Ľ�Ŀ![]() ÿ��ѧ����ѡ��ֻ��ѡ�������Ŀ�е�һ��
ÿ��ѧ����ѡ��ֻ��ѡ�������Ŀ�е�һ��![]() ����������������²�������ͳ��ͼ
����������������²�������ͳ��ͼ![]() ������ͼ�ṩ����Ϣ���ش��������⣺
������ͼ�ṩ����Ϣ���ش��������⣺
![]() ��ϲ���������Ŀ����______�ˣ�ͼ��
��ϲ���������Ŀ����______�ˣ�ͼ��![]() ______��
______��
![]() �벹ȫ����ͳ��ͼ��
�벹ȫ����ͳ��ͼ��
![]() ���ݳ���������������У��1800��ѧ����������Ƹ�У�ж�����ѧ����ϲ���������Ŀ��
���ݳ���������������У��1800��ѧ����������Ƹ�У�ж�����ѧ����ϲ���������Ŀ��
![]() ��ȫ��ͬѧ�У��мס��ҡ���������ͬѧ��ϲ���������Ŀ�������δ���Ӽס��ҡ�������4��ͬѧ��ѡȡ2�˲μ�ѧУ��֯������֪ʶ�����������б�������״ͼ��ͬʱѡ�мס�����ͬѧ�ĸ��ʣ�
��ȫ��ͬѧ�У��мס��ҡ���������ͬѧ��ϲ���������Ŀ�������δ���Ӽס��ҡ�������4��ͬѧ��ѡȡ2�˲μ�ѧУ��֯������֪ʶ�����������б�������״ͼ��ͬʱѡ�мס�����ͬѧ�ĸ��ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
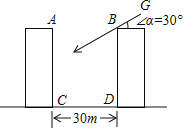
����Ŀ����������¥֮��ľ���CD=30�ף�¥AC��BD��Ϊ10�㣬ÿ��¥��3�ף�
��1������ijʱ�̣�̫������GB��ˮƽ��ļн�Ϊ30�����˿�B¥��Ӱ������A¥�ĵڼ��㣿
��2����̫��������ˮƽ��ļн�Ϊ���ٶ�ʱ��B¥��Ӱ�Ӹպ�����A¥�ĵײ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
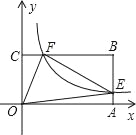
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�����OABC�Ķ���A��C�ֱ���x���y����������ϣ�����������y=![]() �ڵ�һ����ͼ��ֱ���OABC�ı�AB��BC�ߵ���E��F����֪BE=2AE���ı��ε�OEBF���������12��
�ڵ�һ����ͼ��ֱ���OABC�ı�AB��BC�ߵ���E��F����֪BE=2AE���ı��ε�OEBF���������12��
��1����k��ֵ��
��2��������OE��Ӧ�ĺ�����ϵʽ��y=![]() �����߶�EF�ij���
�����߶�EF�ij���
��3���ڣ�2���������£�����AC����֤����EF��AC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�ж�����A�ؿ���B�أ�һ����ͨ�г���B�ؿ���A�أ�������������ʻ��ͬʱ����������ͨ�г���ʻ��ʱ��Ϊx��Сʱ��������֮��ľ���Ϊy��ǧ�ף�����ͼ�е����߱�ʾy��x֮��ĺ�����ϵ������˵������ȷ���ǣ���������
��AB�������1000ǧ�ף�������������3Сʱ����������ͨ�г����ٶ���100ǧ��/Сʱ���ܶ�����A�ص���B�ص�ʱ����4Сʱ��
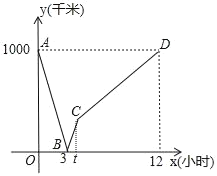
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����²��ϣ�Ȼ�����������⣺��ֱ֪��l1��y����2x��2��ֱ��l2��y����2x+4��ͼ��ʾ�����Կ���ֱ��l1��l2����ֱ��l2������ֱ��l1����ƽ��6�����ȵ�λ�õ���ֱ��l2������ֱ��l1����ƽ��3�����ȵ�λ�õ�����������ֱ��l2�ĺ�������ʽ��������ֱ��l1�ĺ�������ʽֱ�ӵõ������������ֱ��l1����ƽ��6�ij��ȵ�λ��õ�l2����l2�ĺ�������ʽΪ��y����2x��2+6����y����2x+4�������ֱ��l1����ƽ��3�ij��ȵ�λ��õ���l2��l2�ĺ�������ʽΪ��y����2��x��3����2����y����2x+4��
��1����ֱ��y��2x��3����ƽ��2�����ȵ�λ�����õ�ֱ�ߵĺ�������ʽ���� ����
��2����ֱ��y��3x+1����ƽ��m��m��0���������ȵ�λ�����õ�ֱ�ߵĺ�������ʽ���� ����
��3����֪��ֱ��y��![]() x+1����ƽ��n��n��0�������ȵ�λ��õ�ֱ��y��
x+1����ƽ��n��n��0�������ȵ�λ��õ�ֱ��y��![]() x+5����n���� ����
x+5����n���� ����
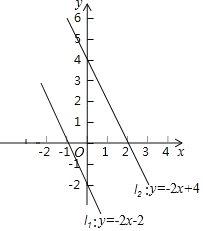
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y��x2��4x��5��x�ύ��A����1��0����B��5��0�����㣬��y�ύ�ڵ�C����P���������ϵ�һ�������C�غϵ�һ�����㣬��S��PAB��S��ABC�����P��������_____
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ����ѧϰ֮�ǣ�����ij�̵깺��A��B�����ľ���Ϊ��Ʒ����֪һ��A���ľߵļ۸��һ��B���ľߵļ۸����5Ԫ������600Ԫ��A���ľߵļ�������400Ԫ��B���ľߵļ�����2����
��1����һ��A���ľߵļ۸�
��2��������Ҫ����У���ڸ��̵깺��A��B�����ľ߹�150����
������A��B�����ľ����辭��W�빺��A���ľߵļ���a֮��ĺ�����ϵʽ��
��������A���ľߵļ���������B���ľ�����2�����Ҽƻ����Ѳ�����2750Ԫ�����м��ֹ��������ҳ��������ٵķ�������������Ҫ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
��![]() ��ֱ����
��ֱ����![]() ��
��![]() ��
��![]() �ֱ���Բ�ཻ��
�ֱ���Բ�ཻ��![]() ��
��![]() ����ô���е�ʽ��һ���������ǣ� ��
����ô���е�ʽ��һ���������ǣ� ��
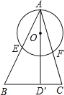
A. AEBF=AFCF B. AEAB=AOAD'
C. AEAB=AFAC D. AEAF=AOAD
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com