
【题目】如图,已知四边形![]() 为矩形,点
为矩形,点![]() 在
在![]() 上(不与
上(不与![]() ,
,![]() 重合),连接
重合),连接![]() ,
,![]() ,以
,以![]() 为一边作正方形
为一边作正方形![]() ,使得点
,使得点![]() 在边
在边![]() 上,给出以下结论:①
上,给出以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() ;其中正确的结论的个数是( )
;其中正确的结论的个数是( )
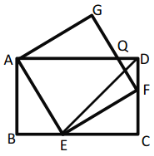
A.1个B.2个C.3个D.4个
【答案】D
【解析】
利用AAS得到△ABE≌△ECF可判断①正确;利用等量代换可判断③正确;证得![]() ,
,![]() ,可判断②正确;可求得∠ADE=45°,∠AQG
,可判断②正确;可求得∠ADE=45°,∠AQG![]() 45
45![]() ,可判断④错误;证得△EFC
,可判断④错误;证得△EFC![]() △AQG,利用等量代换可判断⑤正确.
△AQG,利用等量代换可判断⑤正确.
∵四边形AEFG为正方形,四边形ABCD为矩形,如图:
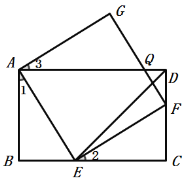
∴∠AEF=∠B=∠C=90°,AE=EF,AB=CD,
∴∠1+∠AEB=90°,∠2+∠AEB =90°,
∴∠1=∠2,
在△ABE和△ECF中,
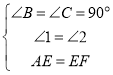 ,
,
∴△ABE≌△ECF(AAS),故①正确;
∴BE=CF,AB=EC,
∴BC+DF= BE+EC+DF = CF+EC+DF= CD+EC= AB+EC=2 EC,故③正确;
∵![]() ,
,
![]() ,
,
∴![]() ,故②正确;
,故②正确;
∵CD= AB=EC,
∴∠CED=∠CDE=∠ADE=45°,
∵∠1+∠EAD=90°,∠3+∠EAD=90°,
∴∠1=∠3,
∵∠AQG=90°-∠3=90°-∠1=90°-∠2,且∠2![]() 45
45![]() ,
,
∴∠AQG![]() 45
45![]() ,
,
∴∠ADE![]() ∠AQG,故④错误;
∠AQG,故④错误;
∵四边形AEFG为正方形,
∴∠G=90°,AG=EF,
∵∠1=∠2=∠3,
∴Rt△EFC![]() Rt△AQG,
Rt△AQG,
∴![]() ,
,
∴![]() ,故⑤正确;
,故⑤正确;
综上,①②③⑤正确,共4个.
故选:D.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
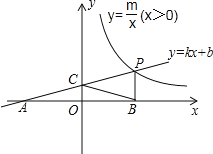
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() (x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(1)求一次函数、反比例函数的解析式;
(2)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,求出点D的坐标;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中抛物线y=﹣x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,3).
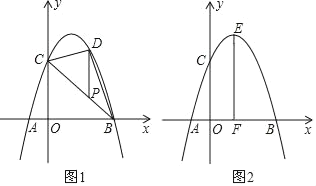
(1)求抛物线的表达式;
(2)如图1,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BCD的面积最大时,求点P的坐标;
(3)如图2,抛物线顶点为E,EF⊥x轴于F点,N是线段EF上一动点,M(m,0)是x轴上一动点,若∠MNC=90°,直接写出实数m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,已知正方形ABCD和正方形AEFG,连接DG,BE.

(1)发现:当正方形AEFG绕点A旋转,如图②所示.
①线段DG与BE之间的数量关系是 ;
②直线DG与直线BE之间的位置关系是 ;
(2)探究:如图③所示,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE时,上述结论是否成立,并说明理由.
(3)应用:在(2)的情况下,连接BG、DE,若AE=1,AB=2,求BG2+DE2的值(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
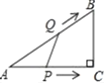
【题目】如图,![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,知道它们都到达点
运动,知道它们都到达点![]() 为止.若
为止.若![]() 的面积为
的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() ,则
,则![]() 与
与![]() 的函数图象是( )
的函数图象是( )
A.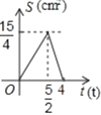 B.
B.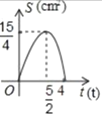 C.
C.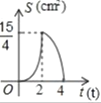 D.
D.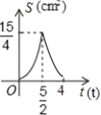
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年新冠病毒在全球蔓延,口罩成为抗击病毒传播的有效物资,某厂需要生产一批口罩,该厂有甲、乙两种型号的生产机器,若用甲机器单独完成这批订单需要消耗原料费76万元,若用乙机器单独完成需要消耗原料费26万元,已知每生产一个口罩,甲机器消耗原料费比乙机器消耗原料费多用0.5元.
(1)求乙机器生产一个口罩需要消耗多少原料费?
(2)为了尽快完成这批订单,该厂决定使用甲、乙机器一起完成这批订单,消耗原料费合计不超过39万元,则乙机器至少生产多少口罩?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙0经过点D,E是⊙O上一点,且∠AED=45°,

(1)求证:CD是⊙O的切线.
(2)若⊙O的半径为3,AE=5,求∠DAE的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感知:如图①,在等腰直角三角形ABC中,∠ACB=90°,BC=m,将边AB绕点B顺时针旋转90°得到线段BD,过点D作DE⊥CB交CB的延长线于点E,连接CD.
(1)求证:△ACB≌△BED;
(2)△BCD的面积为 (用含m的式子表示).
拓展:如图②,在一般的Rt△ABC,∠ACB=90°,BC=m,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,用含m的式子表示△BCD的面积,并说明理由.
应用:如图③,在等腰△ABC中,AB=AC,BC=8,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,则△BCD的面积为 ;若BC=m,则△BCD的面积为 (用含m的式子表示).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com