
【题目】抛物线![]() 经过点A(-1,0)、B(4,0),与y轴交于点C(0,4).
经过点A(-1,0)、B(4,0),与y轴交于点C(0,4).
(1)求抛物线的表达式;
(2)点P为直线BC上方抛物线的一点,分别连接PB、PC,若直线BC恰好平分四边形COBP的面积,求P点坐标;
(3)在(2)的条件下,是否在该抛物线上存在一点Q,该抛物线对称轴上存在一点N,使得以A、P、Q、N为顶点的四边形为平行四边形?若存在,求出Q点坐标,若不存在,请说明理由.
【答案】(1)![]() ;(2)点P坐标为(2,6);(3)Q点坐标为(
;(2)点P坐标为(2,6);(3)Q点坐标为(![]() ,-
,-![]() )或(
)或(![]() ,
,![]() ).
).
【解析】(1)把A、B、C三点坐标代入抛物线y=ax2+bx+c中,求出a、b、c的值即可;
(2)设P点坐标为(x,-x2+3x+4),根据四边形COBP的面积=S△COP+ S△BOP以及四边形COBP的面积=2S△COB求解即可;
(3)分AQ和AN分别为对角线时进行讨论可得解.
(1)把A(-1,0)、B(4,0)、C(0,4)三点坐标代入抛物线y=ax2+bx+c得,
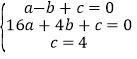 ,
,
解得: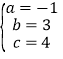
故抛物线的表达式为:y=-x2+3x+4;
(2)设P点坐标为(x,-x2+3x+4),如图,
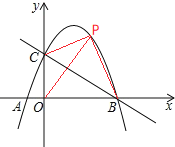
∴四边形COBP的面积=S△COP+ S△BOP=![]() =-2x2+8x+8
=-2x2+8x+8
∵直线BC平分四边形COBP的面积
∴四边形COBP的面积=2S△COB
即:-2x2+8x+8=![]()
解得x=2
将x=2代入抛物线表达式得y=6
故点P坐标为(2,6)
(3)存在
①当AQ为平行四边形的对角线时,Q点横坐标为![]() ,
,![]()
故Q(![]() )
)
②当AN为平行四边形的对角线时,Q点横坐标为![]() ,
,![]()
故Q(![]() )
)
综上所述,Q点坐标为(![]() )或(
)或(![]() )
)


科目:初中数学 来源: 题型:
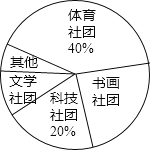
【题目】某校计划成立学生社团,要求每一位学生都选择一个社团,为了了解学生对不同社团的喜爱情况,学校随机抽取了部分学生进行“我最喜爱的一个学生社团”问卷调查,规定每人必须并且只能在“文学社团”、“科学社团”、“书画社团”、“体育社团”和“其他”五项中选择一项,并将统计结果绘制了如下两个不完整的统计图表.
社团名称 | 人数 |
文学社团 | 18 |
科技社团 | a |
书画社团 | 45 |
体育社团 | 72 |
其他 | b |
请解答下列问题:
(1)a= ,b= ;
(2)在扇形统计图中,“书画社团”所对应的扇形圆心角度数为 ;
(3)若该校共有3000名学生,试估计该校学生中选择“文学社团”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知:如图1,在△ABC中,∠ABC的平分线与∠ACB的平分线交于点O,求证:∠BOC=90°+![]() ∠A;
∠A;
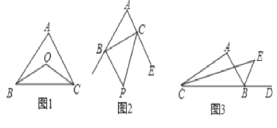
(2)如图2,在△ABC中,BP,CP分别是△ABC的外角∠DBC和∠ECB的平分线,试探究∠BPC与∠A的关系.
(3)如图3,在△ABC中,CE平分∠ACB,BE是△ABC的外角∠ABD的平分线,试探究∠BEC与∠A的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() 平分
平分![]() ,
,![]() .
.
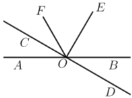
(1)求![]() 的大小,根据下列解答填空(理由或数学式)
的大小,根据下列解答填空(理由或数学式)
解:∵![]() (已知),
(已知),
∴![]() ______°,
______°,
∵![]() ,
,
∴![]() .
.
∵![]() 平分
平分![]() (已知),
(已知),
∴![]() ______
______![]() .
.
∵![]() (______),
(______),
∴![]() ______°.
______°.
(2)直接写出图中所有与![]() 互余的角.
互余的角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.
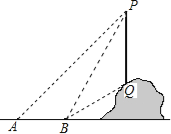
(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度(结果精确到1m).
备用数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为顺利通过“文明城市”验收,盐城市政府拟对部分地区进行改造,根据市政建设需要,须在16天之内完成工程.现有甲、乙两个工程队,经调查知道:乙队单独完成此工程的时间是甲队单独完成此工程时间的2倍,若甲、乙两队合作只需12天完成.
(1)求甲、乙工程队单独完成这项工程各需要多少天?
(2)两队合作完成此项工程,若甲队参与施工a天,乙队参与施工b天,试用含a的代数式表示b;
(3)若甲队每天的工程费用是0.6万元, 乙队每天的工程费用是0.25万元,请你设计一种方案,既能按时完工,又能使工程费最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知2a﹣1的平方根是±3,3a+b﹣9的立方根是2,c是![]() 的整数部分,求a+2b+c的值.
的整数部分,求a+2b+c的值.
(2)有四个实数分别为32,![]() ,
,![]() ,
,![]() .
.
①请你计算其中有理数的和.
②若x﹣2是①中的和的平方,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.
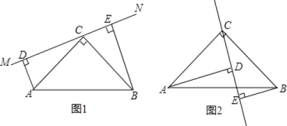
(1)求证:①△ADC≌△CEB;②DE=AD+BE.
(2)当直线MN绕点C旋转到图2的位置时,DE、AD、BE又怎样的关系?并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com